報酬感受性のパラメータをイジって予測誤差大きくなるか確認してみたよ

報酬感受性と報酬予測誤差

前回の記事で、報酬感受性が高まると予測誤差が高まるという話をしました。んで、報酬感受性ρにオピオイドが関わるかもねって話をしました。

ただ、報酬感受性が高い個人の報酬予測誤差が高くなるという記述をしたのですが、本当かそれ？って自分の論理を疑問に思いました。てことで、Q学習式モデルのシミュレーションデータ作って、それぞれのパラメータをイジって、本当に報酬感受性が高いと、Q学習式において、報酬予測誤差が大きくなるのかを検証していきます。

確率選択課題をコンピュータにやらせましょう

強化学習を人間にやらせるときには、2腕バンディット課題と呼ばれたり確率選択課題と呼ばれたりする課題を大抵使用します。

確率選択課題では、◯と△という刺激を参加者にに提示して◯もしくは△の選択をさせます。参加者が◯を選ぶと、80%で報酬のフィードバック、20%で報酬なしのフィードバックを得られます。一方△を選ぶと、確率を入れ替えて、20%で報酬のフィードバック、80%で報酬なしのフィードバックを得られます。課題によっては、報酬なしのフィードバックのところが罰のフィードバックになります。

以下の図1の実験図は修論の図を少し改変したものです。その図の学習セッションが上に書いたものです。修論では、罰ありに設定して、70%, 30%の刺激ペアAB、60%, 40%の刺激ペアCDになっています。投稿したら読んでくだしゃい。

図1. 確率選択課題

今回は、刺激ペア多いとめんどくさいし、テストセッションに興味ないし、パラメータ多いとめんどくさいので、標準的な80%で報酬のフィードバック20%で報酬なしのフィードバックを得られる刺激Aと20%で報酬のフィードバック80%で報酬なしのフィードバックを得られる刺激Bのペアを利用してシミュレーションしていきます。

行動価値Qは以下2つの式で更新します。

\[ δ(t) = r(t) · ρ - Q_i(t) \]

\[ Q_i(t+1) = Q_i(t) + α · δ(t) \]

ただし、まあ当然ながら選択しなかった刺激jについての行動価値は、以下の式で維持して更新。

\[ Q_j(t+1) = Q_j(t) \]

上記式では、tは試行数を意味します。全ての式において(t)になってるのは、t試行目のその値を意味します。(t+1)になってるのは、t+1試行目のその値を意味します。シミュレーション時には、最大試行数100にしときます。r(t)はt試行目のフィードバックを意味します。報酬時には1を、報酬なし時には0を符号化します。お次はパラメータについて。δは、予測誤差を意味します。δは報酬予測誤差、ρは報酬感受性、あと、Q_iは選択した刺激iの行動価値を意味します。

次は、行動価値を実際の行動選択にどのように使用するかを計算します。

\[ P_A(t) = \frac{1}{1 + exp( -β · (Q_A(t) - Q_B(t)))} \]

実際に刺激を選択するときには、上記ソフトマックス関数を元に、βを1に固定した以下の式で、選択確率を算出。βとρをフリーパラメータにすると、識別不能わけわからなくなるので、βを1に固定します。

\[ P_A(t) = \frac{1}{1 + exp( - (Q_A(t) - Q_B(t)))} \]

P_A(t)は、t試行目の、Aの選択確率です。P_Bは1-P_Aで出せますし、上の関数の行動価値の場所交換でもよしです。

よし！式の説明終わり！

さて、シミュレーションデータを作っていきましょう。

シミュレーションデータを作ります

おまじないを言います。

rm(list = ls())
library(ggplot2)
library(dplyr)

## 
##  次のパッケージを付け加えます: 'dplyr'

##  以下のオブジェクトは 'package:stats' からマスクされています:
## 
##     filter, lag

##  以下のオブジェクトは 'package:base' からマスクされています:
## 
##     intersect, setdiff, setequal, union

library(tidyr)
library(htmlTable)
set.seed(1)

実験の試行数や刺激の性質を設定

機械君にやってもらう、刺激選択の試行数と、選択刺激の報酬フィードバックの性質を設定しておきます。

##　試行数について
trial <- 100

## 選択刺激の報酬フィードバックの確率設定
#刺激Aについて
######報酬の確率を0.8に設定
A_probability <- 0.8

#刺激Bについて
######報酬の確率を0.2に設定
B_probability <- 0.2

パラメータチュニチュニします

まずはパラメータをチューニングしていきます。

## alphaの値を設定する。
alpha_input <- c(0.1, 0.5, 0.9)
## rhoの値を設定する。
rho_input <- c(1, 5, 9)

alpha_length <- length(alpha_input)

rho_length <- length(rho_input)

以上のR内の<- を書き換えてあげたら、パラメータを調整できます。具体的には、「alpha <- 〇〇」のところと、「rho <- ◯◯」のところです。

今回は、αを0.1, 0.5, 0.9、ρを1, 5, 9で設定してあげます。

で、設定したパラメータの値の組み合わせ全部を行列にします。

## 学習率alphaのパラメータ作成

alpha　<- rep(alpha_input, each = rho_length)

## 感受性rhoのパラメータ設定
rho <- rep(rho_input, times = alpha_length) 




## idを設定する
id <- c(1:(alpha_length * rho_length))
  
###### alphaとrhoのセットを作る。
parameter_DF <- cbind(id, alpha, rho) %>% data.frame(.)

以上でチュニチュニして、パラメータの行列というかデータフレームを作りました。

データフレームの中身はこんな感じです。αは0.1, 0.5, 0.9が存在します。それぞれのαに、ρは1, 5, 9が存在します。最終的に、3列3 × 3 (=9)行の配列というかデータフレーム。ついでに、各パラメータにidをつけときました。idは9種類あります。

DT::datatable(parameter_DF)

ついでに、各パラメータは100試行することにしているので、各行を100個リピートしておきます。

ids <- rep(id, each = trial)
alphas <- rep(alpha, each = trial)
rhos <- rep(rho, each = trial)

trials <- rep(1:trial, times = alpha_length * rho_length)
##simulation_DFという名前でデータフレーム作っとく。
simulation_DF <- cbind(ids, alphas, rhos, trials) %>% data.frame(.)

##ついでに、simulation_DFにQ値と、刺激の選択確率(P_A)と、行動価値(Q_A, Q_B)、予測誤差(delta)と、選択行動の履歴(choice,Aを選んだ場合1、Bを選んだ場合2を符号化)と、選択刺激から得られたフィードバック(feedback,報酬時には1を罰時には-1を符号化)と、行動選択のログを付け足しておく。
##変数の意味(変数名,変数の符号化の補足説明)

simulation_DF <- simulation_DF %>%
  mutate(.,
         P_A = rep(
           0,
           times = alpha_length  * rho_length * trial
           ),
         Q_A = rep(
           0, 
           times = alpha_length * rho_length * trial
           ),
         
         Q_B = rep(
           0, 
           times = alpha_length * rho_length * trial
           ),
         
         delta = rep(
           0, 
           times = alpha_length * rho_length * trial  
           ),
         
         choice = rep(
           0, 
           times = alpha_length * rho_length * trial 
           ),
         
         feedback = rep(
           0, 
           times = alpha_length * rho_length * trial 
           ),
         
         )

シミュレーションの簡単な説明

半年くらい前に、階層ベイズでQ学習頑張らねばと備忘録書いていた時の、rスクリプトを参考にシミュレーションしていきます。

まずは、以下のソフトマックスのβを1に固定した式で、行動価値から計算した刺激選択の確率を計算します。

\[ P_A(t) = \frac{1}{1 + exp( - (Q_A(t) - Q_B(t)))} \]

次に、選択した刺激に紐づいた確率的なフィードバックを与えます。これは、Aを選んだら80%で報酬を、残り20%で報酬なしを与え、Bを選んだら20%で報酬を、残り80%で報酬なしを与えます。

次に、以下のそれぞれの式で、今回得られた確率的なフィードバックに感受性を掛け合わせたエージェントにとってのその報酬あるいは罰の主観的な価値の大きさから行動価値を引いた予測誤差を以下の式で出します。

\[ δ(t) = r(t) · ρ - Q_i(t) \]

最後に以下の式で、予測誤差を学習率で更新して強化学習をしていきます。

\[ Q_i(t+1) = Q_i(t) + α · δ(t) \]

ただし、選択されなかった刺激jは、以下の式で維持更新されます。

\[ Q_j(t+1) = Q_j(t) \]

上記の処理を、idごとに、for文で100試行分処理してあげます。なんかもっとスマートな方法ある気がしますが、僕は心理学科でR触ってる雑魚なのでこんなもんで許してくれ。

##エージェントごとに分けていく。

for(n in id) {
  id_simulation_DF <- simulation_DF %>% filter(., ids == n)
  ###試行ごとにfor文
  for(t in 1:trial) {
    id_simulation_DF$P_A[t] <- 
      1/
      (
        1 + exp( 
        -1 *(id_simulation_DF$Q_A[t] - id_simulation_DF$Q_B[t])
        )
      )
    ####提示された刺激の行動価値に応じた行動選択の確率を算出して、
    ####その確率に応じた行動選択をしていく。
    if( runif(1,0,1) < id_simulation_DF$P_A[t] ) {
      ##runif(◯, △, □)は、[△ ~ □]範囲の乱数を◯個生成する。
      id_simulation_DF$choice[t] <- 1
      id_simulation_DF$feedback[t] <- runif(1,0,1) < A_probability %>% 
        as.numeric(.)
    }
    else{
      id_simulation_DF$choice[t] <- 2
      id_simulation_DF$feedback[t] <- runif(1,0,1) < B_probability %>% 
        as.numeric(.)
    }
    
    ###行動価値の更新
    if(t < trial){
      ####Aを選択した場合
      if(id_simulation_DF$choice[t] == 1){
        id_simulation_DF$delta[t] <- id_simulation_DF$feedback[t] * 
          rho[n] - id_simulation_DF$Q_A[t]
        id_simulation_DF$Q_A[t+1] <- id_simulation_DF$Q_A[t] + 
            alpha[n] * id_simulation_DF$delta[t]
        id_simulation_DF$Q_B[t+1] <- id_simulation_DF$Q_B[t]
      }
      #####Bを選択した場合
      else{
        id_simulation_DF$delta[t] <- id_simulation_DF$feedback[t] * 
          rho[n] - id_simulation_DF$Q_B[t]
        id_simulation_DF$Q_B[t+1] <- id_simulation_DF$Q_B[t] + 
            alpha[n] * id_simulation_DF$delta[t]
        id_simulation_DF$Q_A[t+1] <- id_simulation_DF$Q_A[t]
      }
    }
    simulation_DF[( trial * (n-1) + 1 ) :( trial * n ), ] <- id_simulation_DF
  }
}

シミュレートされたデータでいい感じの作図をば

全データで分析

上でシミュレーションしたデータを元に作図をしていきましょう。 x軸に試行数を、y軸にδを、色の違いでρを、形の違いでαを表現した散布図を書きます。頑張れ、ggplot2::geom_point()!!!!

all_rhos_color_point <- simulation_DF %>% 
  ggplot(
    aes(
      x = trials,
      y = delta,
      shape = factor(alphas),
      color = factor(rhos)
    )
  ) + 
  geom_point()

print(all_rhos_color_point)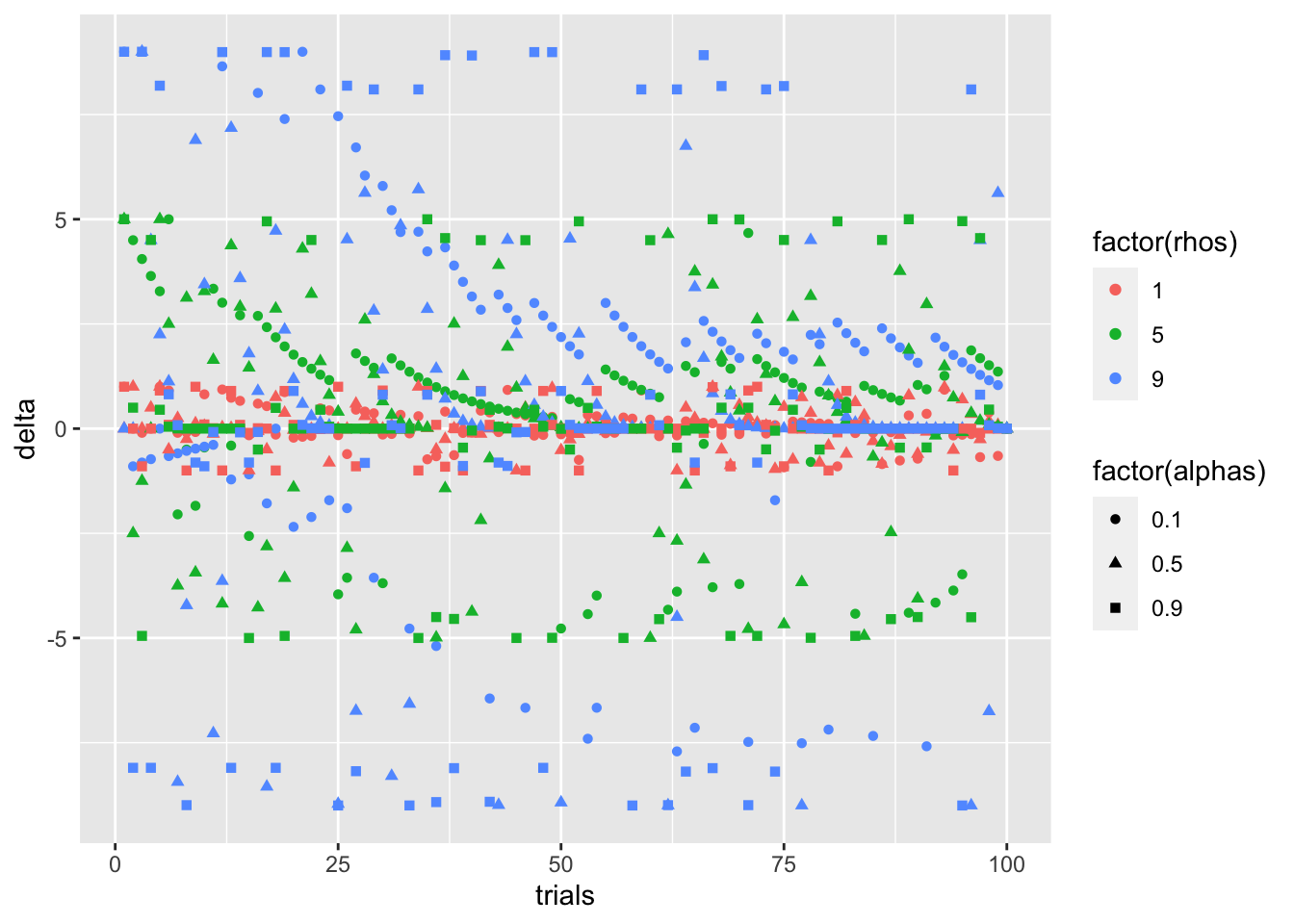

色(α)がδの高さを予測するかの確認に、色と形を入れ替えてみます。

all_alphas_color_point <- simulation_DF %>% 
  ggplot(
    aes(
      x = trials,
      y = delta,
      shape = factor(rhos),
      color = factor(alphas)
    )
  ) + 
  geom_point()

print(all_alphas_color_point)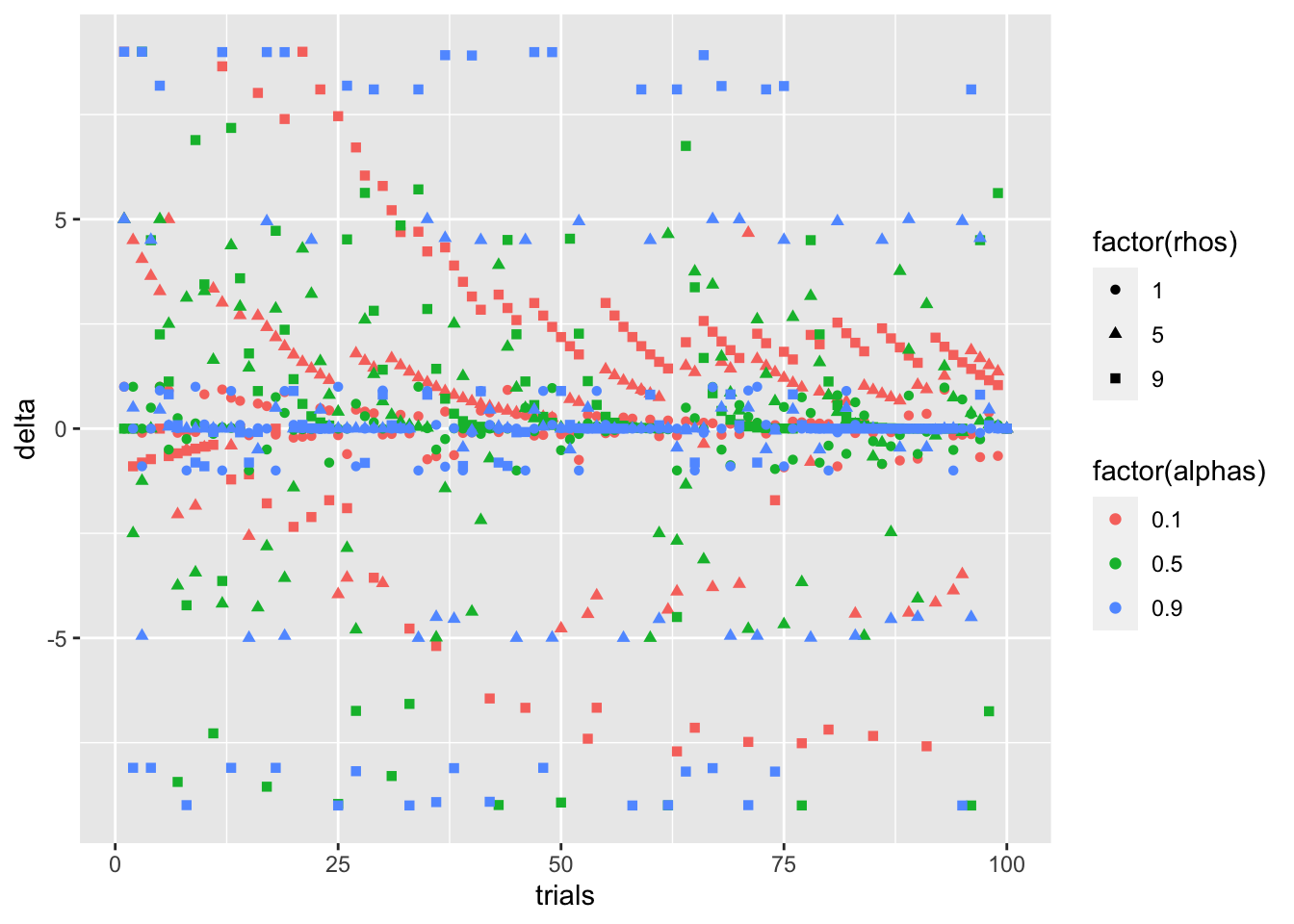

まあ、見て分かる通り、ρの方が、δの値の高さを予測してそうですね。

記述統計をとってみると、

##mean
with(simulation_DF, tapply(delta, list(rhos, alphas), mean))

##          0.1        0.5          0.9
## 1 0.07052153 0.02167533 0.0001111111
## 5 0.44897548 0.10037284 0.0555055051
## 9 0.96037435 0.12374998 0.1008919001

おっと、δの平均値だけ見ると、ρの高さが、δの大きさを予測してなさそうですね。

ただ、図と合わせてみると、正の値であれ負の値であれδの絶対値の大きさに、ρが効きそうですね。絶対値の大きい正と絶対値の大きい負の値を足し合わせたから、0に近づいちゃったのかもしれません。

てことで、以下の処理。

報酬が得られなかった試行を取り除く

僕は報酬が得られた時に関心があるので、報酬なし時の試行を取り除いて作図と記述統計再度してみます。

only_gain_trial_simulation_DF <- simulation_DF %>%
  filter(., feedback == 1)

色がρ、形がαです。色(ρ)がδを予測してそうですね。

only_gain_rhos_color_point <- only_gain_trial_simulation_DF %>% 
  ggplot(
    aes(
      x = trials,
      y = delta,
      shape = factor(alphas),
      color = factor(rhos)
    )
  ) + 
  geom_point()

print(only_gain_rhos_color_point)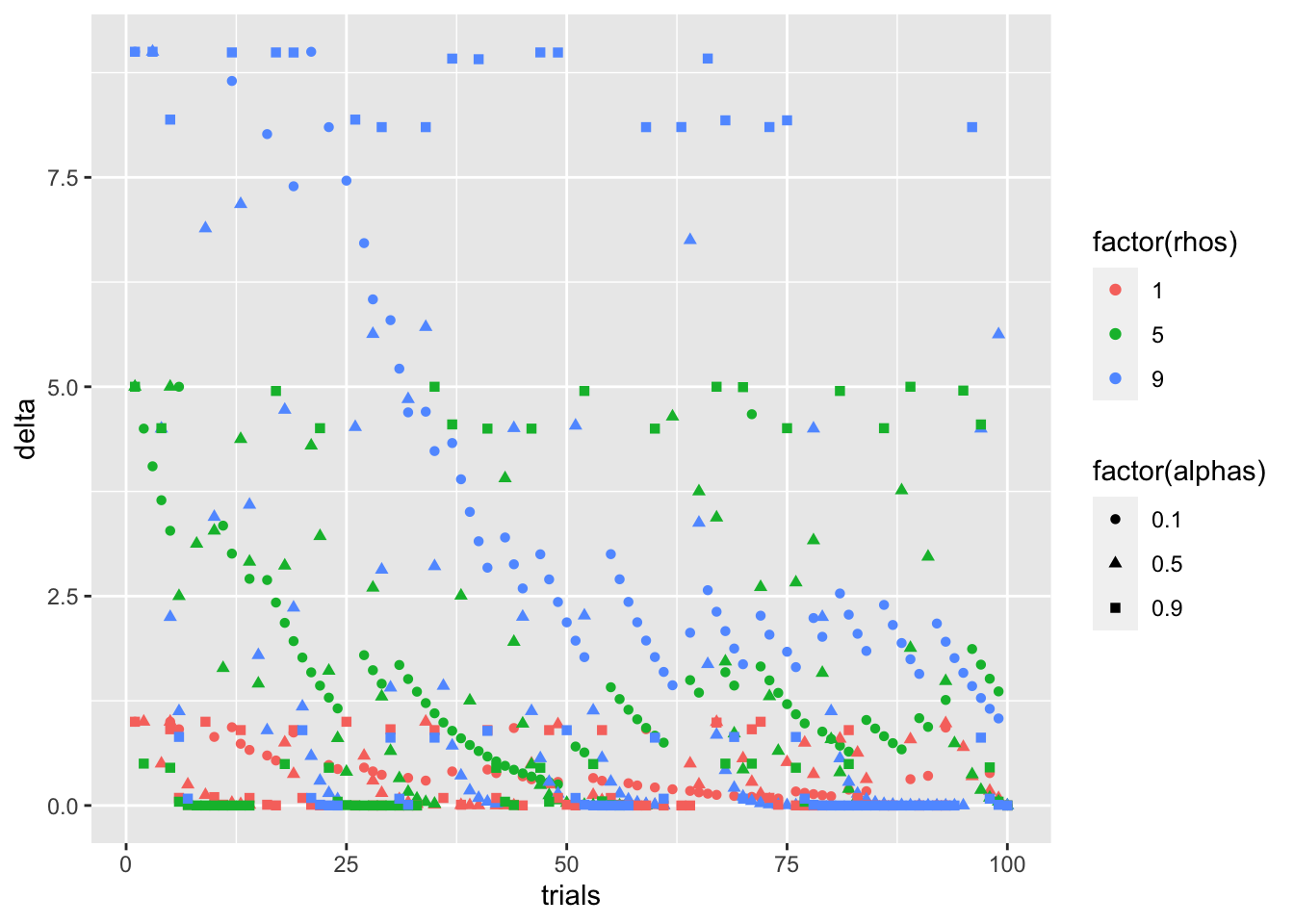

色と形を入れ替えます。今度は、色(α)は、δを予測してる気配はないですね。

only_gain_alphas_color_point <- only_gain_trial_simulation_DF %>% 
  ggplot(
    aes(
      x = trials,
      y = delta,
      shape = factor(rhos),
      color = factor(alphas)
    )
  ) + 
  geom_point()

print(only_gain_alphas_color_point)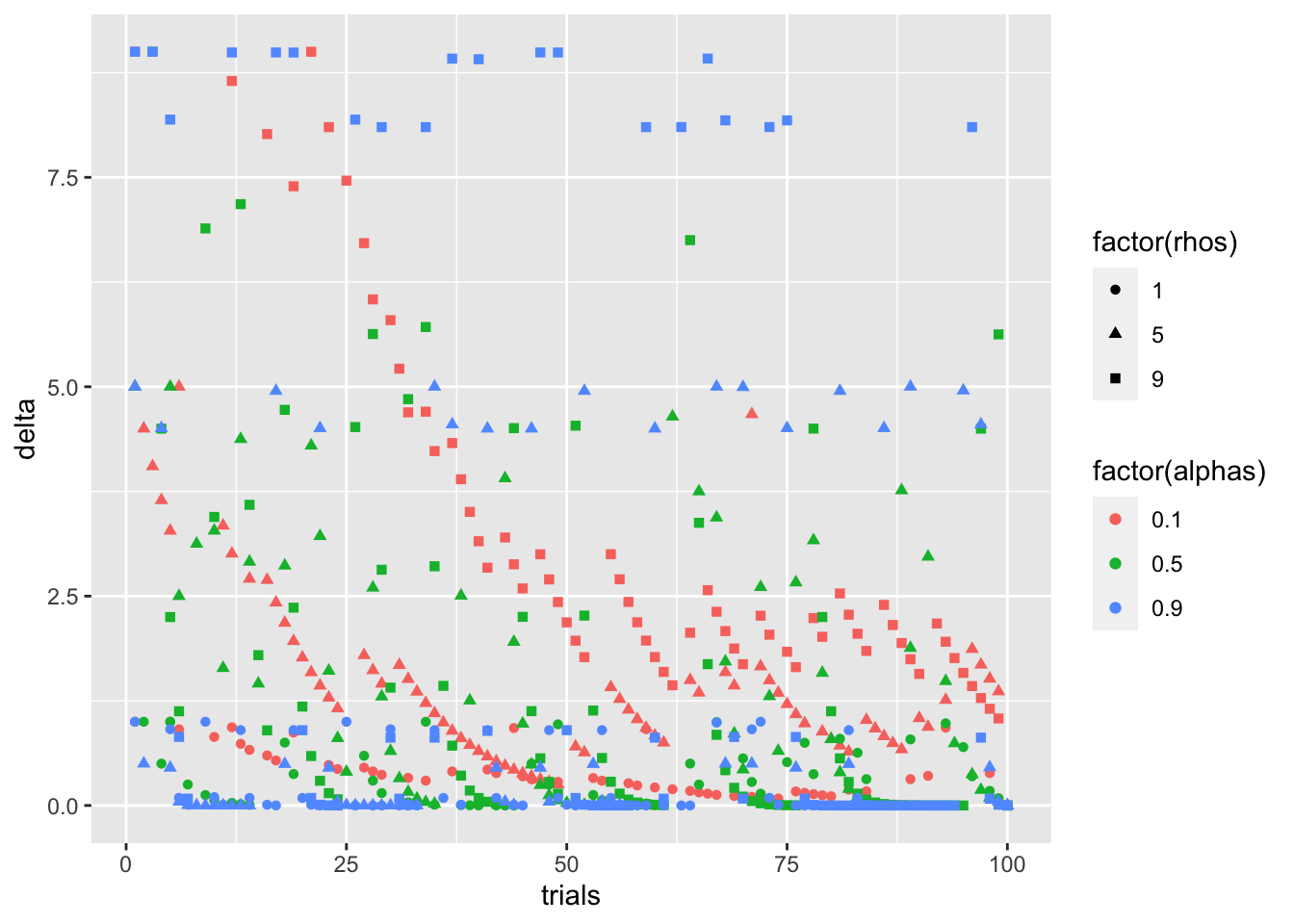

ついでに記述統計。

##mean
with(only_gain_trial_simulation_DF, tapply(delta, list(rhos, alphas), mean))

##         0.1       0.5       0.9
## 1 0.4000534 0.3247109 0.2424182
## 5 1.4844282 1.4568255 1.5767352
## 9 3.1528438 1.6004510 2.6887691

報酬が得られなかった試行を取り除いたら、つまりδが負になる試行を取り除いたら、全試行では陰に隠れていたρの強烈なδへのパワーが現れましたね。

報酬感受性ρがδの予測誤差を修飾していることが確認されました。動機づけを生み出すドパミンは、他のパラメータで修飾されているかもしれませんね。気持ちよさ(hedonic)を生み出すモルヒネがドパミンの修飾パラメータだと僕は思いました。まあ強化学習とかQ学習とか数理的な背景は置いておいても、報酬得られた時にその主観的な気持ちよさが大きくなれば、そりゃその行動の動機づけ高まりますよね、多分。そいえば、射精時の主観的な気持ちよさが、オピオイド拮抗薬を入れたら下がったり(Murphy et al. 1990)するんで、まあ報酬それ自体の気持ち良さの修飾にオピオイド効いているような気はします。強化学習の報酬の文脈とはズレるけども。

あと、すっごいどうでもいい後書きなんですけど、αを「あるふぁ」と打って変換で入力していたのですが、いっぱい「あるふぁ」を打っていたら、アルファタウリにF1頑張ってほしいなって思いました。すっごいどうでもいい後書き失礼しました。

追記(3/16)

サンプルコード

ここまでチャンクで書いたスクリプトは、こちらからダウンロードできます。

ρやαの値をいじりたい場合は、

rho_input <- c(1, 5, 9)

と

alpha_input <- c(0.1, 0.5, 0.9)

の値をいじってください。

最終的に出来上がったデータフレーム

P_AやQ_A,Q_B,deltaの生データを見たい方用に機械君が頑張った結果のシミュレーションデータを貼っておきます。

DT::datatable(simulation_DF)

引用文献

Murphy, Michael R., Stuart A. Checkley, Jonathan R. Seckl, and Stafford L. Lightman. 1990. “Naloxone inhibits oxytocin release at orgasm in man.” Journal of Clinical Endocrinology and Metabolism 71 (4). https://doi.org/10.1210/jcem-71-4-1056.

Takuto-Psych/報酬感受性のパラメータをイジって予測誤差大きくなるか確認してみたよ