Mathmatical Principles of Reinforcement 強化の数学的原理(MPR)におけるarousal覚醒の意味を説明する

MPRにおける一番最初の基本原理は、Arousal覚醒だそうです。覚醒とは、強化子の提示によって行動が活性化されることだそうです。条件づけの最も根幹になる要素です。

今回の記事では Killeen and Sitomer (2003) の論文でまとめられている実験やその要旨を見てどのように原理のモデルが作られたのかを確認してきます。

一日一回の食事

まずは、1日1回ハトに餌を与えてみましょう。その時の活動量を計測すると、給餌直後に最も活動が高まり、その後は急速に活動量が下がるそうです。ここでいう活動というのは、オペラント条件づけの対象になるようなレバー押しといった行動ではなく飼育小屋やスキナー箱の内部での徘徊といった行動を指します。

そしてその活動の様子はこんな式で表現できるそうです。

\[ b(t) = b_1 * e^ {\frac{-t}\alpha} \]

ここで、それぞれの文字は以下のような意味を持ちます。

b₁：切片。切片というよりも感覚的には給餌直後の1分間の活動量ですね。
t：給餌後の時間経過。単位は秒。
α ：時間定数。時間の経過を調整する定数とでも捉えています。
e：ネイピア数

グラフにするとこんな感じ。給餌後は最も活動的で、その後段々と活動量が減衰していくんですね。

##なんのパッケージ使ってるかを示すために、見えるようにしておきます。
rm(list = ls())
library(tidyverse)

## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr     1.1.4     ✔ readr     2.1.5
## ✔ forcats   1.0.0     ✔ stringr   1.5.1
## ✔ ggplot2   3.5.2     ✔ tibble    3.3.0
## ✔ lubridate 1.9.4     ✔ tidyr     1.3.1
## ✔ purrr     1.0.4     
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag()    masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

activity_fun <- function(alpha = 6, beta_1 = 9.7, t){
  b_t <- beta_1 * (exp(1) ^ (- t / alpha))
  return(b_t)
}
DF_activity <- data.frame(
  time_minute = seq(from = 0, to = 13, by = 0.1)
  ,responses_per_minute = activity_fun(t = seq(from = 0, to = 13, by = 0.1))
)
DF_activity %>% ggplot(
  aes(x = time_minute, y = responses_per_minute)
) + geom_line()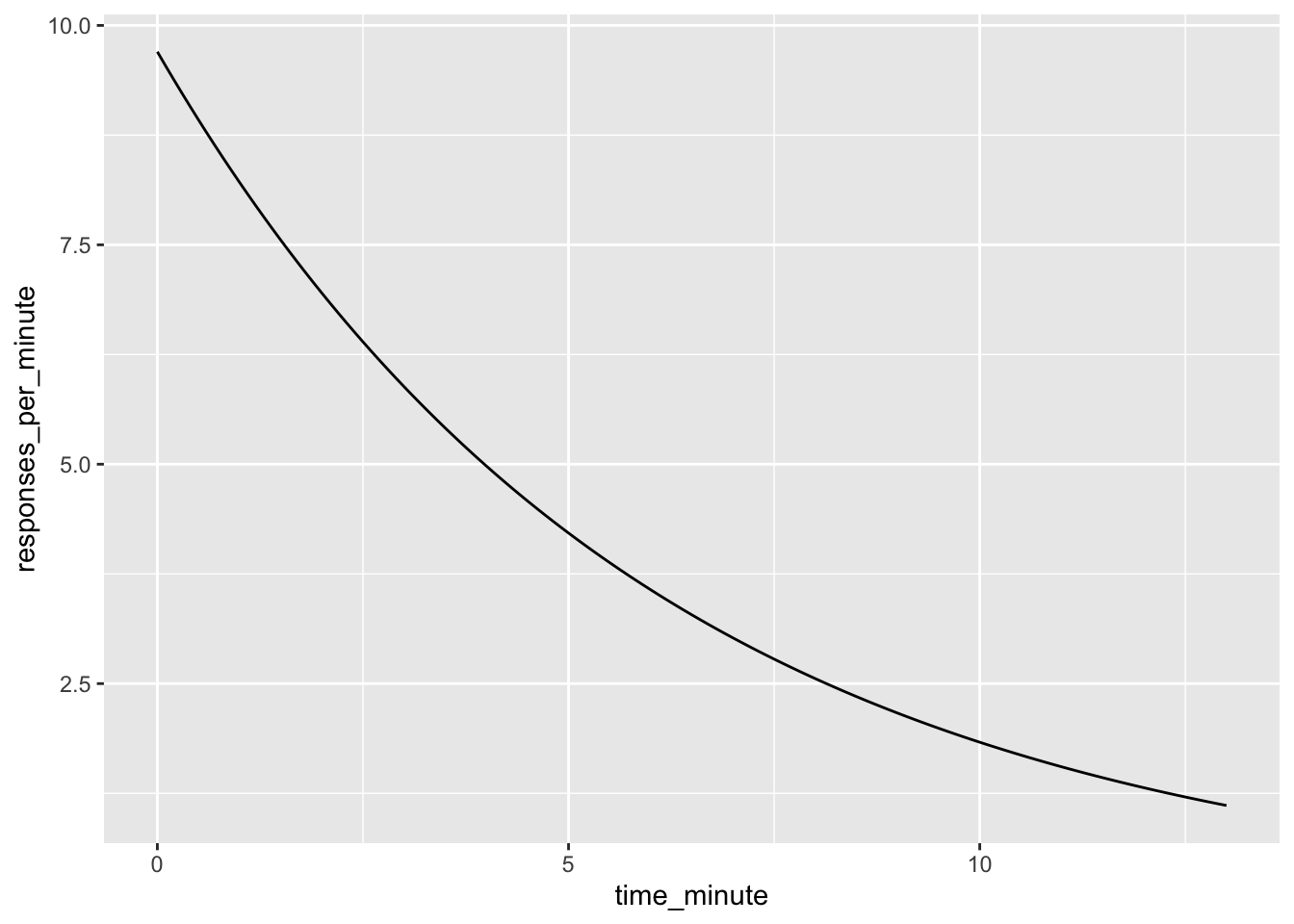

直感的にも納得いきます。毎日決まった時刻にご飯が出てくるだけの環境にいると、ご飯が出てきた直後にだけ活動レベルが高まり、その後、急激に活動レベルが減衰していく。特に飼ったことはないですが、人間とコミュニケーションを取るとは考えられていない愛玩動物を飼育したら、こんな挙動をしそうですね。カエルでも飼ってみようかな。

〇〇秒ごとに餌を与えてみる

次に、給餌の頻度を上げてみたらどうなるでしょうか。給餌の頻度が上がると、これまでの給餌経験が増えるに従って段々と活動レベルが上がるそうです。

wikiにも元の論文(Killeen and Sitomer 2003)にも特に式は触れられていないですが、多分こんな感じの式になっています。大元の実験の論文にあたるべきなのでしょうがちょっと今は読む余裕がない。後日読んでおきます。

\[ b(n) = b_1 * (1 - e^ {\frac{-n}\alpha}) \]

b₁：切片。切片というよりも感覚的には給餌後の活動量の上限ですね。
n：これまでに連続で何回給餌されたか
α ：何らかの定数。これまでの給餌履歴を調整する定数とでも捉えます。
e：ネイピア数

今回のこの給餌の頻度をあげるという環境側の操作は、あくまで固定時間を操作して、その時間が経過した後に勝手に餌が出てくるようにするというだけです。そのため、何らかのオペラント行動を求めた望ましい行動に対しての強化という性質のものではないです。こういった被験者の行動とは独立したスケジュールをFixed Time（固定時間）スケジュールと呼ぶそうです。知らんかった。

では、この関数に従って、給餌履歴を元にした活動量の推移を描いてみましょう。こんな感じになります。

##さっきの関数を流用する
DF_reward_history <- data.frame(
  n = 1:30
  ,FT30 = 60 - activity_fun(
    alpha = 5
    ,beta_1 =  60 
    ,t = 1:30
  )
  ,FT50 = 60 * 3 / 5 - activity_fun( ##あとで出てくる原則に従って上限設定してるよ。
    alpha = 5
    ,beta_1 =  60 
    ,t = 1:30
  )
) %>% pivot_longer(
  cols = - n
  ,names_to = "variable"
  ,values_to = 'responses_per_minute'
)

DF_reward_history %>% ggplot(
  .
  ,aes(x = n, y = responses_per_minute, colour = variable)
) + geom_line()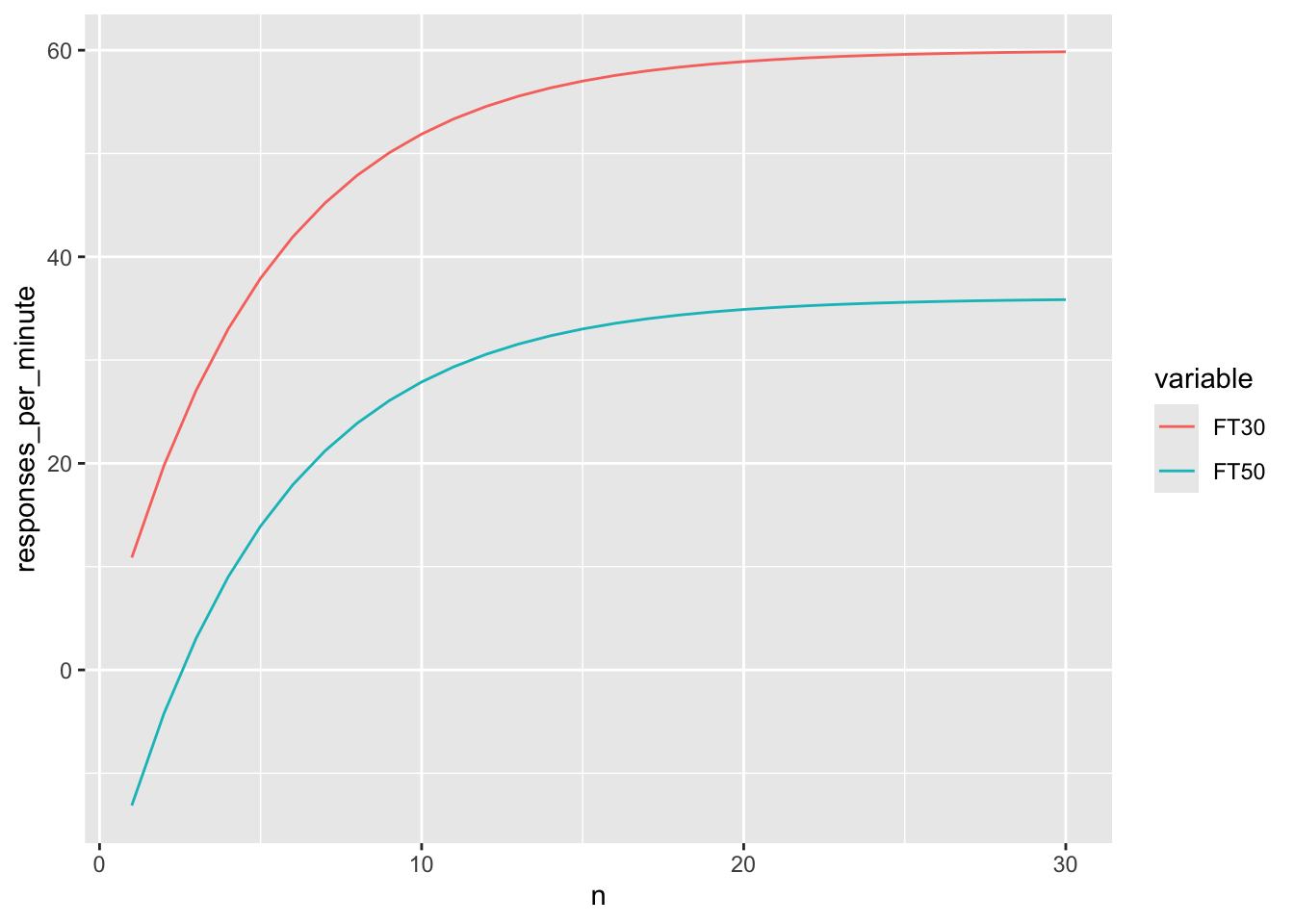

なるほど。

固定時間で餌が出てくると時間間隔が狭い方が、活動量の上限は高いようです。まあこれは一番最後に式を書きますので、ここでは触れません。

また、これまでの給餌経験の回数の累積に対して、最初は急速に活動上昇が生じ、その後は上限が来てしまうという動きをするそうです。

確かに、何となく理解はできます。仮に僕が禁固刑に行って決まった時刻に（だいたい5時間おきかな）にご飯もらえたとしたら、ご飯もらった回数が増えていくに従って室内徘徊頻度上がりそうですね。どっかで上限があるでしょうが。

さて、何となく直感的にこんなグラフになりそうだなというのは納得できたのですが、Killeenさんはこの結果には問題があるという指摘をして追加の実験をしました。

その問題とは、給餌をすることで自発的な活動が上昇することは、実は迷信的な行動を学習した結果かもしれないというものです。

本来FTスケジュールなので、被験者が動こうが動かなかろうが、それに関係なく餌が出てきます。にもかかわらず、被験者が何か動いた後に餌が出てきてしまったとしたら、その餌は謎の動きを迷信的に引き起こす強化子になってしまうかもしれません。ちなみに、僕もそんな環境にいたら服を脱いだ後に腕立て伏せをすると思います。異常独身男性の完成です。

人間に当てはめてみたら笑えますが、動物とは会話ができないので迷信的に行動が増えているのかどうかを実験デザインの工夫で検証しなくてはなりません。

〇〇秒ごとに餌を与える。ただし、給餌前に反応したら「待て」だ

Killeenさんは、そんな迷信的な行動の増加を「待て」を使って制御しました。

具体的には、FT〇〇secの〇〇秒経過時点で被験者が動いていた場合には5秒間餌を与えないことにしたそうです。こういった手続きをDROというそうです。

この操作により、餌の提示直前に被験者は自発的な活動をしなくなります。もしこの制御が完璧に効いたとしたら、活動が完全になくなるかもしれません。結果はどうだったでしょうか。

結果はこんなグラフになりました。

##式の説明の前に関数書いているので順番は逆だけど、図が欲しいので
general_activity_fun <- function(C = 25, TI = 5, A = 50, t){
  R = A * (
    (exp(1)^ (-t/C)) - (exp(1)^ (-t/TI)) 
  )
  return(R)
}

DF_general_activity <- data.frame(
  time = seq(from = 0, to = 2 * 60, by = 0.1)
  ,responses_per_min = general_activity_fun(
    t = seq(from = 0, to = 2 * 60, by = 0.1)
  )

) 
DF_general_activity %>% ggplot(
  aes(x = time, y = responses_per_min)
) + geom_line(
)

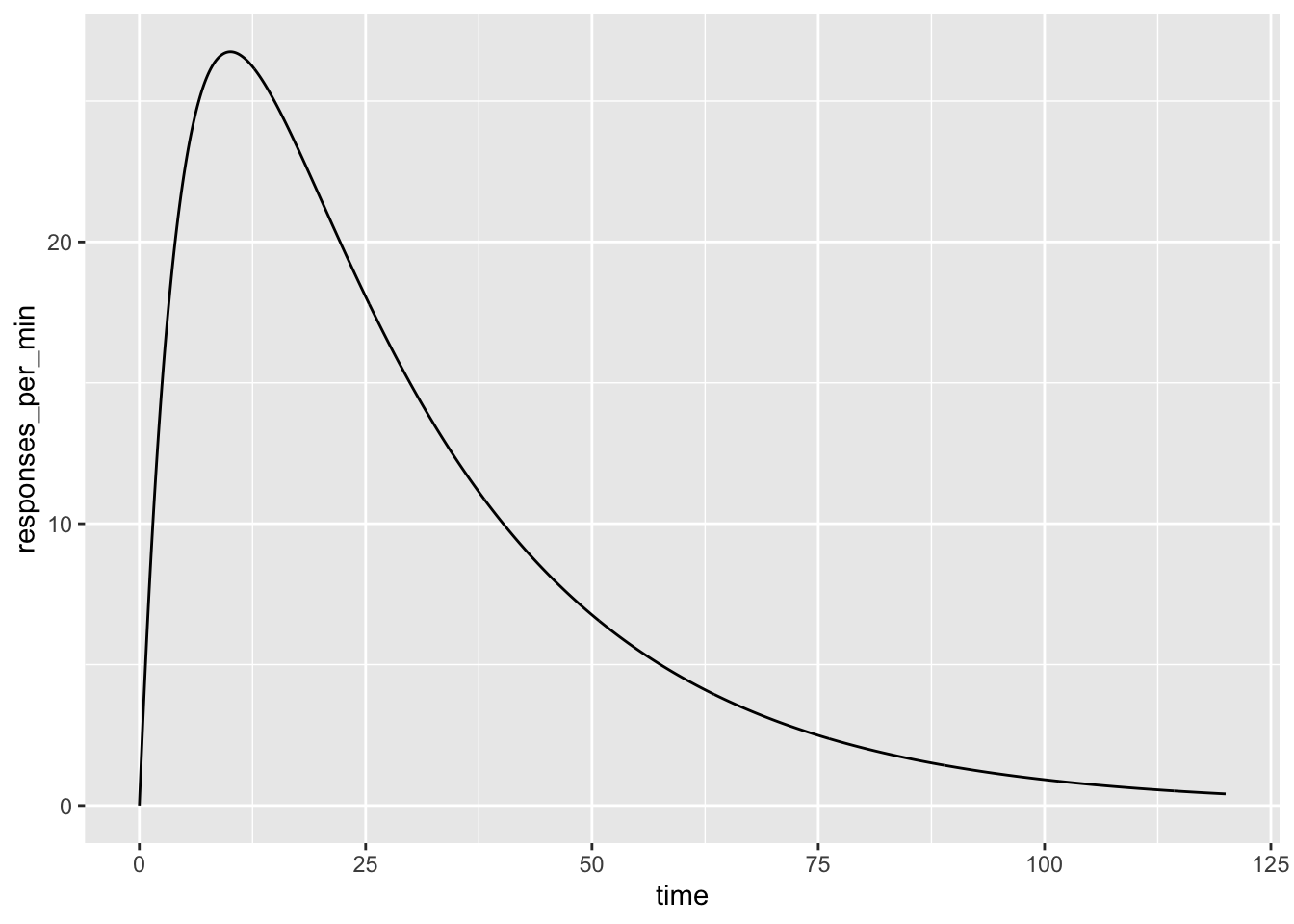
このグラフの横軸は、直前に給餌されてから何秒経ったかを意味します。一方、縦軸は、1分間の平均活動量。また、ここで計測している活動というのは、（元論文に当たっていないので多分ですが）床の上での徘徊を指しています。

さて、給餌直後には活動の減少が見られます。なぜなら、ここではホッパー（餌の受け皿）の周りを探すといったような餌に対しての目標志向的な行動が現れるためです。このような行動を行うと、スキナー箱の中での徘徊というような活動は減少し、その記録は床の感圧板には記録されません。だから、「活動」は減っているわけですね。

一方、少し経ってからは、活動は上がります。これは、そういった目標志向的な行動が時間経過で減ってきて、「活動」に移行したことを示します。その後は活動は下がっていきます。これは、待て（DRO）によって、要らない動きをしてしまうと、給餌をお預けされてしまうために生じるわけです。

さて、この時間と活動のグラフは実は、餌が持っている活動性を高めるという効果と、待て（DRO）による活動低下の効果を合わせた結果だと考えられます。それを表現したのが以下のグラフです。

DF_general_activity <- data.frame(
  time = seq(from = 0, to = 2 * 60, by = 0.1)
  ,R = general_activity_fun(
    t = seq(from = 0, to = 2 * 60, by = 0.1)
  )
  ,TI = activity_fun(
    alpha = 25
    ,beta_1 = 50
    ,t = seq(from = 0, to = 2 * 60, by = 0.1)
  )
  ,C = 50 - activity_fun(
    alpha = 5
    ,beta_1 = 50
    ,t = seq(from = 0, to = 2 * 60, by = 0.1)
  )
) %>% pivot_longer(
  cols = - time
  ,names_to = "variable"
  ,values_to = 'value'
)
DF_general_activity %>% ggplot(
  aes(x = time, y = value, colour = variable)
) + geom_line()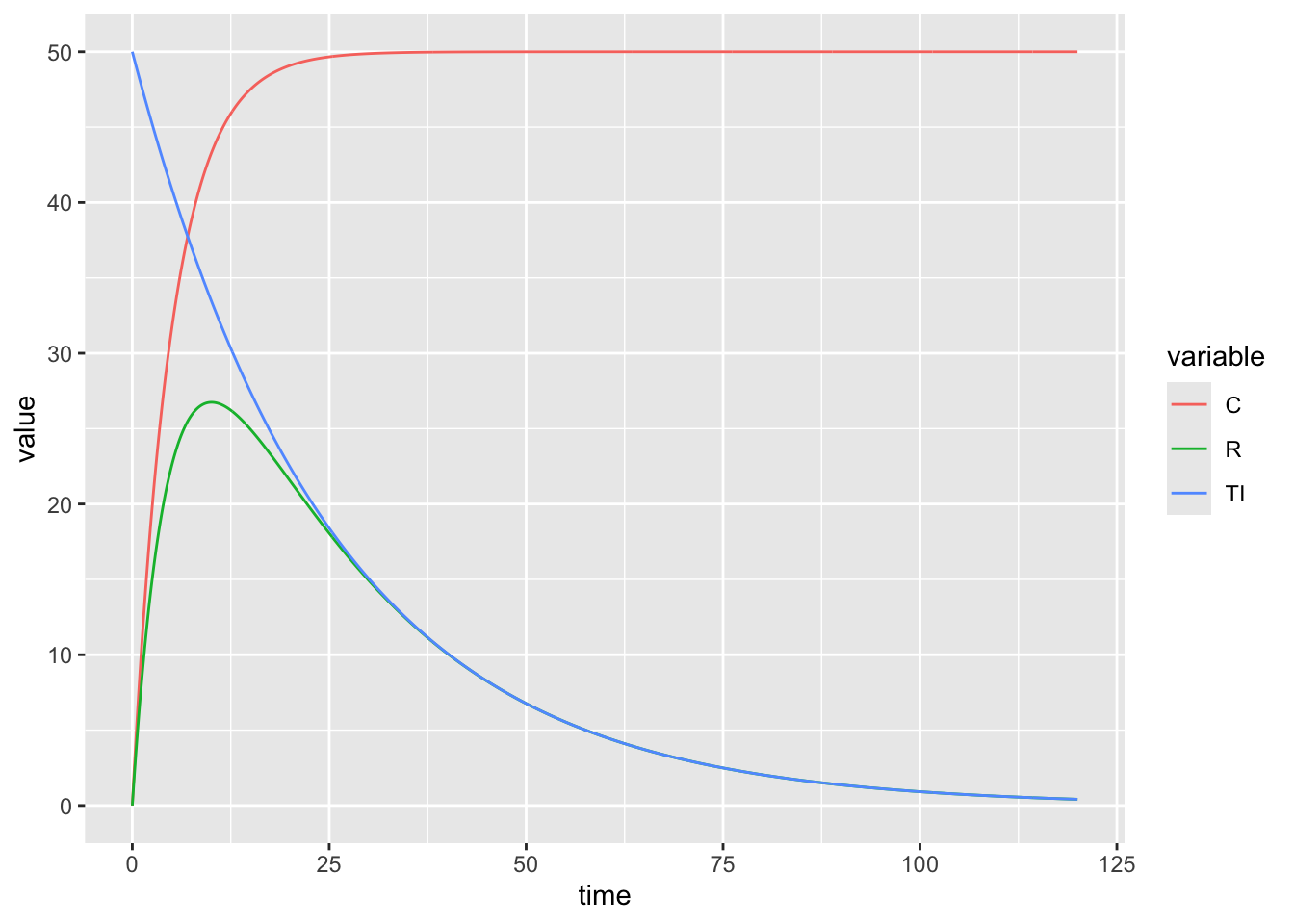

先ほどのグラフは緑の線です。赤は、活動に対しての競合の行動（ホッパーを漁ったり）、青は時間によって生じる活動レベルの減衰です。この赤と青のグラフを合わせたものとして、緑のグラフが出来上がると Killeen and Sitomer (2003) は表現しました。僕はこのセンテンスと式を論文で見て理解ができた時にかなりテンションが上がりました。まあ理解するのに20hかかりましたけども。

緑がこの式

\[ R = A × (e^{\frac{-t}C} - e^{\frac{-t}I}) \]

R：活動

A：覚醒

I：時間的な抑制

C：競合する他の行動

それを生み出すための赤と青の式も書いておきます。

赤の式

\[ R_{red} = A × (1- e^{\frac{-t}I}) \]

青の式

\[ R_{blue} = A × e^{\frac{-t}C} \]

活動の量の上限は給餌の頻度に対して線形に増加する

ここまで、給餌後にどのように活動が減衰するかを見てきました。

最後に、どのように活動の上限が決められているかを見ていきます。結論はシンプルで、活動量の上限は、給餌の頻度に比例するというものです。

式としては、こんな感じです。

\[ A = a r \]

A：覚醒の度合い
a：特異的活性化
r：給餌の頻度

最終的なこの式の理解としてはシンプルなのですが、ここに至るまでの導出も書いておきます

\[ A =A_1*\alpha r(1-e^{-n/\alpha r}) \]

A：覚醒の度合い
A₁:一度目の強化子提示による覚醒の高まり（２個目のグラフの切片と捉えて良いかな）
α：時間定数。時間の経過を調整する定数とでも捉えています。
r：給餌の頻度
n：これまでの累計の給餌回数

さて、この式のnが増えていくとどうなるでしょうか。

\[ (1-e^{-∞/\alpha r}) = 1 \]

になります。念のためRの出力見ておきましょう。

1 - exp(1)^-(Inf/10)

## [1] 1

このため、この式のnを増やしてくと、最終的には以下のような式になります。

\[ A_∞ = A_1 \alpha r \]

さて、A₁α=aという代入をしてあげると以下のとてもシンプルな式になりました。

\[ A = a r \]

この式でグラフを描くと以下のようになります。まあ、式の通りですね。綺麗な線形だ。

元の論文を読んでもらっても、この図は綺麗な線形で感動できます。

DF_upper_limit <- data.frame(
  reinforces_per_min = 0:12
  ,responses_per_min = 50 * (0:12)
)

DF_upper_limit %>% ggplot(
  .
  ,aes(x = reinforces_per_min, y = responses_per_min)
) + geom_point()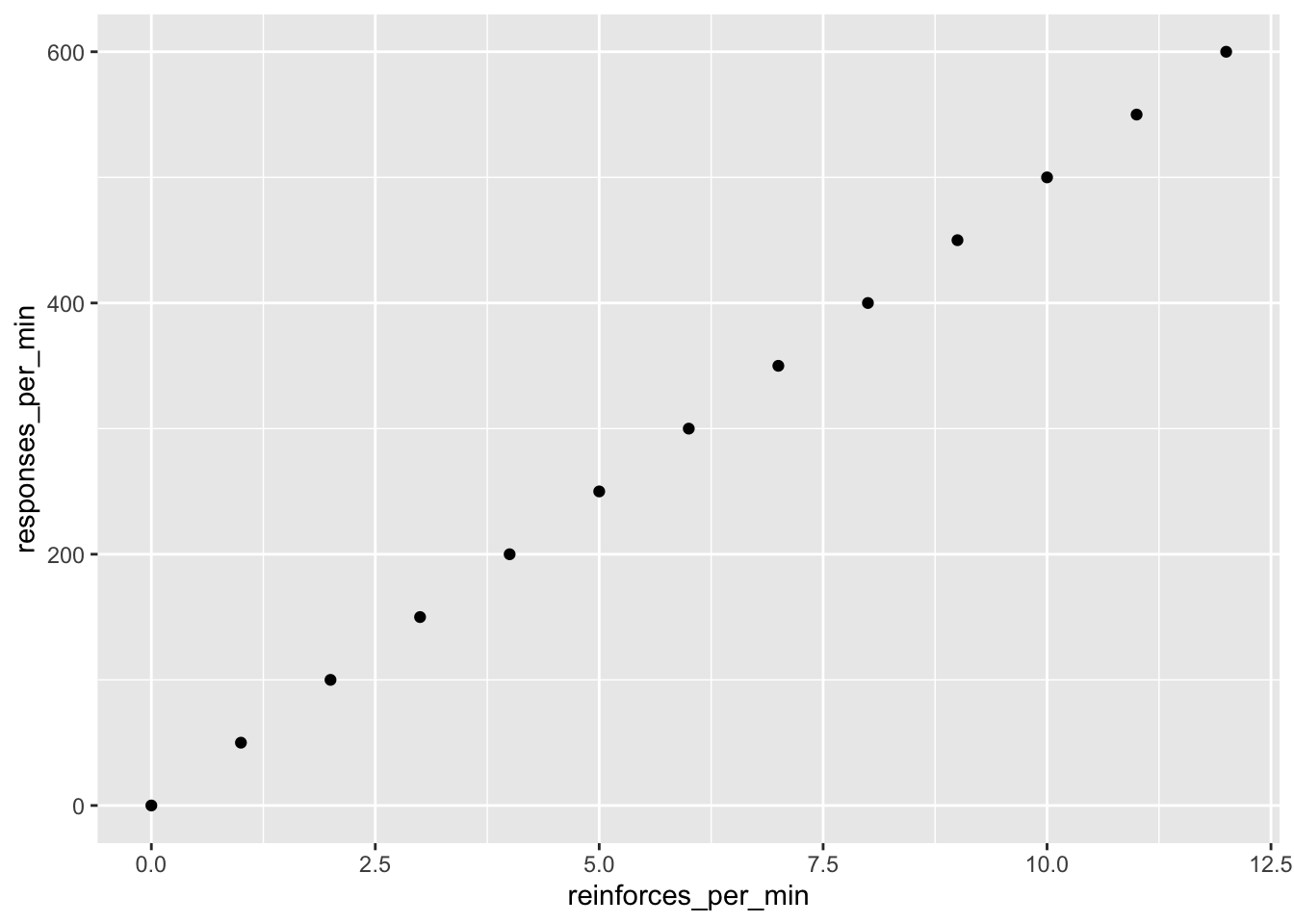

この給餌（強化）の頻度を上げるという操作によって、覚醒の度合いが線形に上がるというのは、MPRにおける一番初めの重要な原理だそうです。

引用文献

Killeen, Peter R, and Matthew T Sitomer. 2003. “MPR.” Behavioural Processes 62 (1): 49–64. https://doi.org/https://doi.org/10.1016/S0376-6357(03)00017-2.

Takuto-Psych/Mathmatical Principles of Reinforcement 強化の数学的原理(MPR)におけるarousal覚醒の意味を説明する

一日一回の食事

〇〇秒ごとに餌を与えてみる

〇〇秒ごとに餌を与える。ただし、給餌前に反応したら「待て」だ

活動の量の上限は給餌の頻度に対して線形に増加する

引用文献