Takuto-Psych/Mathmatical Principles of Reinforcement 強化の数学的原理(MPR)におけるConstraint 制約の意味を説明する

IRT 反応間間隔とresponse rate反応率の関係性

arousal 覚醒と反応率の関連性

さて、arousalと反応率の関係性について Peter R. Killeen et al. (2002) は以下の関係性を発見しました。

その発見とは、1/τ は、覚醒レベルAと相関するということでした。また、前回の記事の最後に書いたように覚醒レベルは、A = arという式で表現されます。これらから以下の式が得られます。aは特定の強化子に対する活性度であるspecific activation、rは、強化子の出現頻度です。

\[ \frac{1}{\tau} = ar \]

さらに式を変形すると、

\[ \tau = \frac{1}{ar} \]

となります。

さて、伝統的に反応率として利用されていた

\[ b = \frac{1}{\delta + \tau} \]

という式に、代入して変形すると、以下の式になります。

\[ b = \frac{r}{\delta r + \frac{1}{a}} \]

この式の分母の左側を見てみましょう。反応には必ず時間を要するため、δrというのは必ず0より大きくなります。一方右側の、1/aについて見てみましょう。aの値が大きくなると、0に近づいていきます。つまり、この分母の最小値は、必ずδの大きさに依存してしまいます。

また、分子のrは、強化の頻度です。

以上より、上で問題点として挙げた通りですが、最大の反応率b_maxは先に示した式のように天井が生じてしまいます。

\[ b_{max} = \frac{1}{\delta r} \]

この関係性をグラフにしておきます。

##なんのパッケージ使ってるかを示すために、見えるようにしておきます。
rm(list = ls())
library(tidyverse)

## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr     1.1.4     ✔ readr     2.1.5
## ✔ forcats   1.0.0     ✔ stringr   1.5.1
## ✔ ggplot2   3.5.2     ✔ tibble    3.3.0
## ✔ lubridate 1.9.4     ✔ tidyr     1.3.1
## ✔ purrr     1.0.4     
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag()    masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

rate_get <- function(delta, r, a){
  b <- r / (delta * r + (1/a))
  return(b)
}
##deltaは生物がマックスの速度で動いているものと捉えるために、固定の0.1秒に設定
DF_rate <- data.frame(
  r = rep(1:10, 100)
  ,a = rep(c(1:10), each = 100)
  ,delta = 0.1
)

DF_rate <- DF_rate %>% mutate(
  .
  ,b = rate_get(delta = DF_rate$delta, r = DF_rate$r, a = DF_rate$a)
)

DF_rate %>% ggplot(
  .
  ,aes(x = a, y = b, colour = r)
) + geom_point()

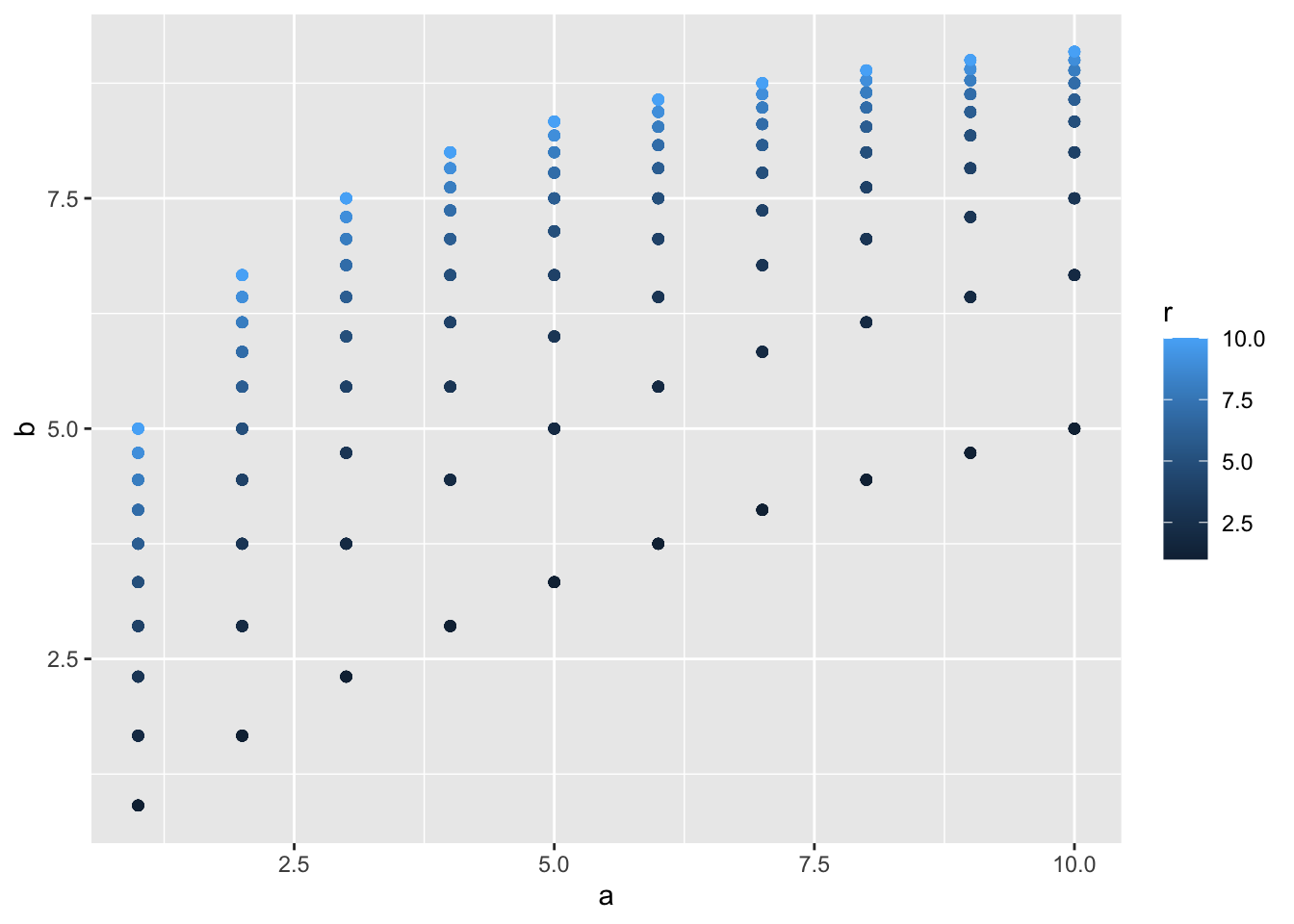
このグラフのように、1/0.1 = 10の天井を超えないような反応率が出てきます。

Constraintとは

\[ b = \frac{r}{\delta r + \frac{1}{a}} \]

この式で示されるMPRの第二の重要な原理とは、反応率bは、「反応に要する時間」δというConstraint 制約が課されるということです。

おまけ IRTの分布を描いてみる

ちなみに、Peter R. Killeen et al. (2002) では、FRスケジュール下での生物の反応についてのIRTの分布を出しています。今手元にラットくんがいないので、Rコードでその分布を描いてみたいと思います。

\[ IRT = \delta + \tau \]

という式ですが、Peter R. Killeen et al. (2002) の実験では、δの値は0.07秒で固定されていますが、その後のτの時間というのは平均的には、0.22秒だったそうです。ただし、τは右の裾野が広いような分布になっていました。つまり、指数関数的な分布になっていたということです。

これらを設定して作図しましょう。

n_resp <- 1e4       # 反応数
delta <- 0.07      # 反応に要する時間 (s)
lambda <- 1/0.22     # delta後の発生率
tau <- rexp(n_resp, rate = lambda)

irt <- delta + tau

# ビンごとに相対頻度を集計 
bin_width <- 0.10
breaks <- seq(0, ceiling(max(irt)/bin_width)*bin_width, by = bin_width)


DF_IRT <- data.frame(
  IRT = irt
) %>% mutate(
  .
  ,bin = cut(IRT, breaks = breaks, right = FALSE)
) %>% count(# 各ビンの度数 
  bin
  ,.drop = FALSE
) %>% mutate(
  rel_freq = n / sum(n) # 相対頻度
  ,bin_center = (as.numeric(bin) - 0.5) * bin_width # ビン中央
  )  

##理論的な指数分布の値を追加しとく。
DF_IRT <- DF_IRT %>% mutate(
  .
  ,theory = ifelse(
    bin_center < delta, 0
    ,lambda * exp(-lambda * (bin_center - delta)) * bin_width
  )
)

ggplot(
  DF_IRT
  ,aes(x = bin_center, y = rel_freq)
) + geom_col(
  fill = "grey80"
  ,colour = "black"
  ,width = bin_width
) + geom_line(
  aes(y = theory)
  ,colour = "red"
  ,size = 1
) +
  scale_x_continuous(
    "IRT (s)"
    ,breaks = seq(0, max(breaks), 0.1)
  ) +
  scale_y_continuous("Relative frequency") +
  labs(title = "Simulated IRT distribution ",
       subtitle = paste("delta =", delta, "s ; tau = ", round(mean(tau), 2), "/s")) +
  theme_bw(base_size = 14)

## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.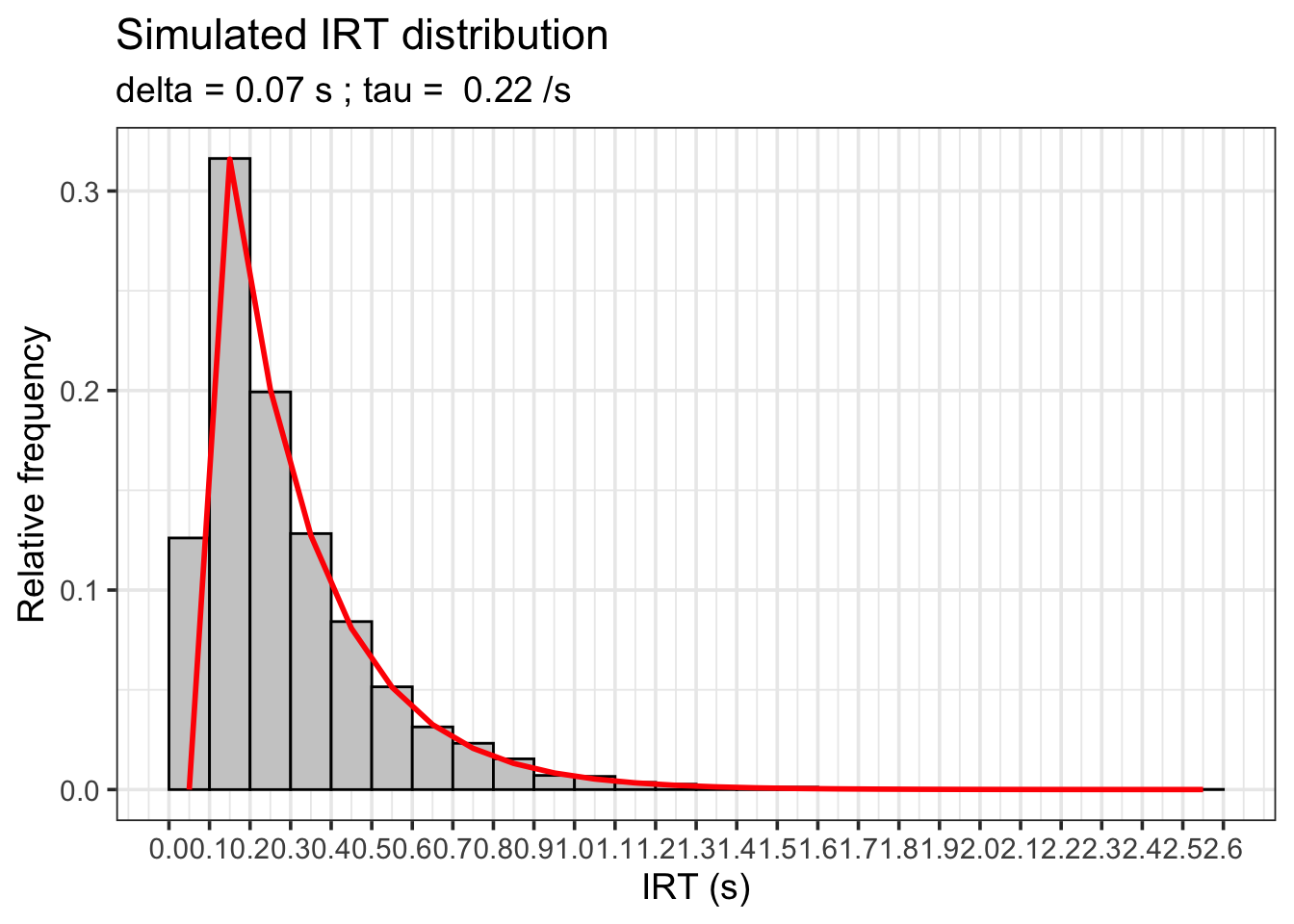

グラフの説明をしておきます。横軸はIRTの長さです。縦軸は、そのIRTの相対的な出現頻度です。

ヒストグラムのbin達は、実際に観測される頻度です。

一方、赤色の線は、τの指数関数的な出現確率に基づいた、理論的な線です。τは、δの時間内に出現するはずがないので、δを超える（このグラフなら0.1を超える）までは生じ得ないため、0.2秒以降に赤色の線が出現します。面白いのが元の論文では、このδのことをrefractory periodと記述しています。まるで神経が反応できないかのような表現ですね。

さて、ヒストグラムのbin達を改めて見ましょう。このグラフを見てみるとよくわかりますが、IRTの出現は、δの秒数の近くに集まります。これが、反応率bは、「反応に要する時間」δという制約が課されるということを行動の観察レベルで確認できるということですね。

まだこの先は読めていませんが、FRは休止が起きやすいわけですが、VRやRRでは休止が起きにくいとされていますよね。環境側のランダムさによって、この指数関数の分布を調整するような操作が効いてきたら、休止が起きにくくなったりしそうですね。