MPRの最後の原理、Coupling 結合について説明していきます。
前回の記事では、IRTを元にした反応率というものについて考えました。IRTを構成する要素には、「反応に要する時間」δと、指数関数的な性質の「真の反応間間隔」τがあるよという内容でした。そして、このIRTを元にした反応率の算出方法では、δが必ず0より大きい値になるという性質による、反応率の上限が生じるという特徴がありました。
Coupling 結合というのは簡単にいうとこの反応率を調整する概念です。この理解を、元論文(Killeen and Sitomer 2003)を元に深めていきます。
強化子と反応との関係性
我々が強化子を提示されて反応が増える時のことを考えてみます。
まずは連続強化CRFについて考えてみます。もしあなたが、目の前のレバーを1回押すと1秒後に空から1円玉が1メートル先に落ちてきたとしましょう。何度やっても、レバーを押すと1秒後に1円玉が降ってきます。このような環境では、「レバーを1回押す」という反応と、1秒後の1円玉という強化子との関係性(随伴性)をcoupling 結合させるわけです。
次に、同じCRFでも少し特殊な環境を考えます。先ほどはレバー押しの1秒後に1メートル先に1円玉が降ってきましたが、今回は、レバー押しの10秒後に1メートル先に1円玉が落ちてきたとします。この時、「レバーを1回押す」という反応と10秒後の1円玉という強化子との関係性(随伴性)の結合は先ほどより弱くなることが予測できます。
これが、MPRの3つ目のCoupling 結合の原則です。その原則とは「反応と強化子の間のcoupling 結合は、両者の間に距離があるほど減少する」というものです。この距離というのは、時間的なものでも、空間的なものでも、間に介在する事象の数でも良いです。たとえば、先のCRFの例ならば10秒後というものだけでなく、1円玉が1メートル先に落ちるのではなく、10メートル先に落ちてくるという環境でも、結合が弱まるということです。そして、この結合は、反応と強化子の間の距離に対して指数関数的に減衰していくものであるという仮定を置くことにします。
また、すべての強化子はその出現前のあらゆる行動を強化し得ます。たとえば、FTスケジュールでよく見られるような迷信的な行動の獲得についても、この結合の考え方で説明ができ得ます。本来一定時間で勝手に強化子が出る環境だとしても、その強化子が出現する前に(時間的に)距離が近かった行動と強化子との間の結合も生じうるということです。ただし、FRやFIといった明確に標的行動を設定しているものよりも、その何らかの迷信的な行動は強化子と距離が空いているので、結合強度が弱くなるわけですね。
ここで重要なのはKilleenは、強化子というのは、記憶の中にあるすべての反応の確率を増加させることによって、その機能を有すると考えていることです。この記憶の中の反応の確率の増やし具合を結合という概念が調整しているのではないかという主張をしているわけです。そしてその結合は、強化子と行動との間の距離が決めているという考えているわけですね。
FRスケジュールの各レバー押しについて考える
さて、このCoupling 結合を、FRスケジュールに当てはめて考えてみましょう。ここではFR5を考えます。
強化子が提示される直前(スキナー箱の設定によってはほぼ同時)に押した5回目のレバー押しというのは、強化との距離を1とします。次に、4回目のレバー押しを強化との距離を2に、同様に計算して、1回目のレバー押しを距離5とします。
この時、強化子は直前に行われていた行動の集まりに対して最大1の連想強度を持ちます。FR5というスケジュールであれば、5回レバーを押すという行動の集まりに対して最大1の連想強度を利用できると捉えるということですね。
さて、5回目のレバー押しについて考えてみるとそれは強化子の1個前の事態です。レバー押しは1の連想強度のうち割合β(0 < β < 1)だけ受け取ることができると考えます。ここで、1個過去の事態という意味でpast1 と表現すると、
\[ {past}_1 = \beta \]
4回目のレバー押しについては、最大の連想強度1から5回目のレバー押しで使われた強度βを引いた(1-β)だけが利用可能になります。その(1-β)にβをかけた
\[ past_2 = β(1-β) \]
が4回目のレバー押しの強度として受け取られます。3回目のレバー押しについても同様に考えると、β(1-β)の残りの分が利用可能になりますが、その差分というのは5回目のレバー押しで利用した残りから引くため以下の式になります。
\[ (1-\beta) - \beta(1-\beta) = (1-\beta)^2 \]
これについて、またβを掛け合わせたものが、3回目のレバー押しの強度になるわけで、以下の通りです。
\[ past_3 = \beta(1-\beta)^2 \]
以上より、これをFRnについてn回目のレバー押しからどれだけ離れているかを意味するpastn の強度について一般化すると以下のようにになります。
\[ past_n = \beta(1-\beta)^ {n - 1} \]
FRnスケジュールでは、レバーを押すという同じ種類の行動がn個集まっていると捉えることができます。このn回ボタンを押すという行動の集まりの結合係数CFRn というのは以下の式のようにその和で表現できます。
\[ C_{FR_n} = \sum \beta(1 - \beta)^n \\= 1 - (1- \beta)^n \]
途中式は以下の通り。等比数列の和の公式なんて、10年ぶりに見た。
さて、CFRnというのは実は、nが十分に大きくなると1に近づきます。上の式について代入して計算してみると、以下の通り。
##使っている関数を明示
library(tidyverse)## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr 1.1.4 ✔ readr 2.1.5
## ✔ forcats 1.0.0 ✔ stringr 1.5.1
## ✔ ggplot2 3.5.2 ✔ tibble 3.3.0
## ✔ lubridate 1.9.4 ✔ tidyr 1.3.1
## ✔ purrr 1.1.0
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag() masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errorsc_FR_fun <- function(
beta = .56
,n
){
c <- 1 - (1 - beta) ^ n
return(c)
}
DF_FR_C <- data.frame(
c = c_FR_fun(n = 1:25)
,n = 1:25
)
DF_FR_C %>% ggplot(
aes(x = n, y = c)
) + geom_line()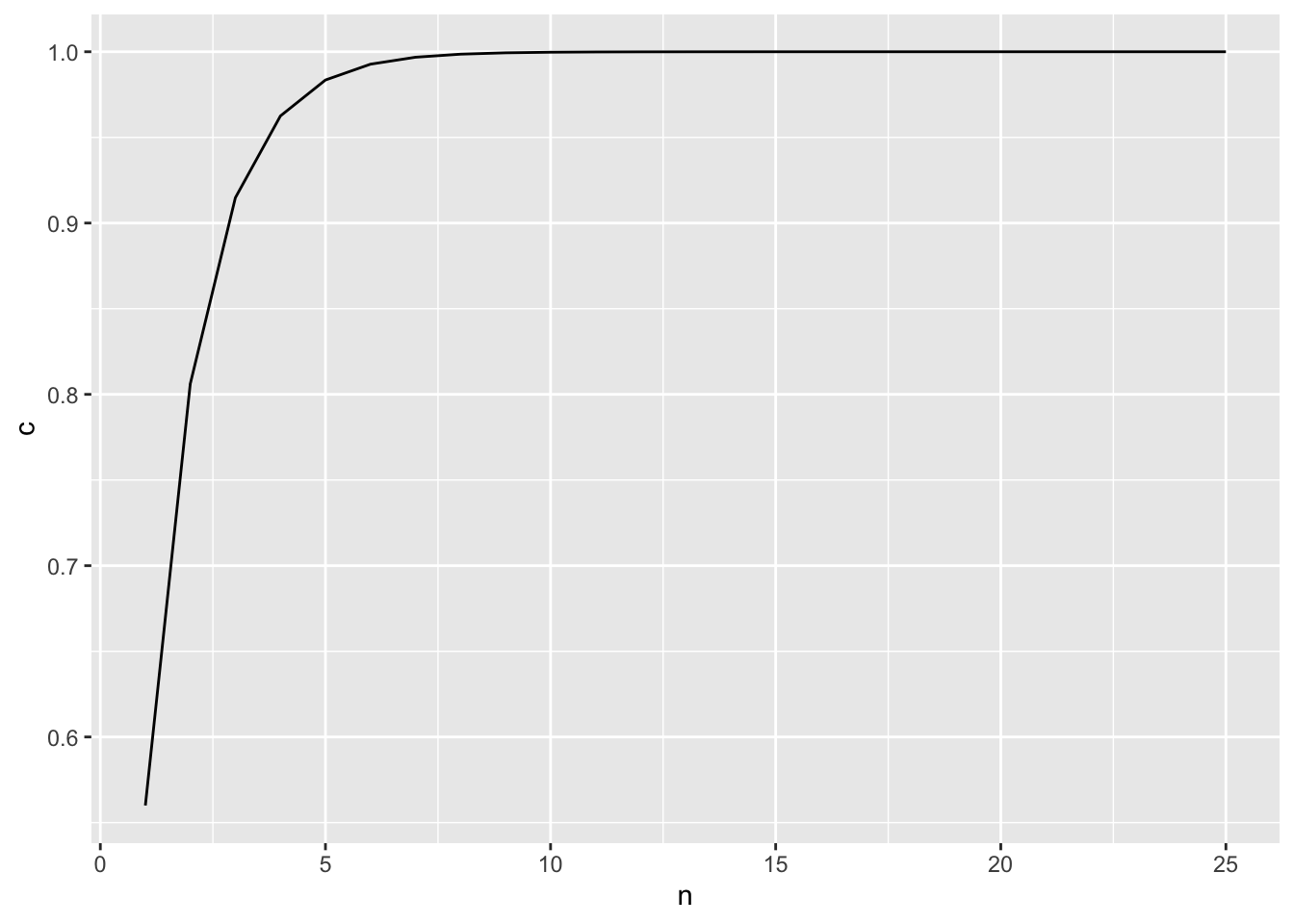
ここまでは、結合の係数がどのように算出されるかをFRを例にCFRn について考えてきました。次はこの結合の係数がどのように反応率に影響をするかを考えます。
結合係数は反応率に対して影響を及ぼす
さて、IRTを元に計算をした反応率について振り返りましょう。
\[ b = \frac{1}{\delta + \tau} \]
という式をいろいろ代入して計算すると、
\[ b = \frac{r}{\delta r + \frac{1}{a}} \]
という式になります。
ここで、反応率をb、反応に要する時間をδ、特異的活性化をa、強化率をrとします。それぞれの意味については、前回の記事でご確認を。
この式に対して、結合 Couplingの係数c.を掛け合わせることで、スケジュールごとの反応率を算出することができるのではないかという提案をKilleenはしています。つまり、以下のような式ですね。
\[ b = \frac{c.r}{\delta r + \frac{1}{a}} \]
ここで、結合係数c.というのは、あくまで仮置きのものであるため「.」という記号をつけているそうです。FRn についての結合係数なら、先に出したようなCFRn というものを代入できるからですね。
だから今回の例なら、
\[ c. = C_{FR_n} = 1 - (1- \beta)^n \]
になります。
ところで、強化率というのは、1秒あたりの強化子提示の回数を意味します。この時、FRnスケジュールにおいては、毎秒何回反応するかという意味のbと組み合わせると、
\[ r = \frac{b}{n} \]
と置くことができます。たとえば、1秒間に16回ボタンを連打することができる名人がいるとして、その名人が仮にFR2スケジュールに従事すれば、1秒間に8回(=16/2)餌を獲得できるということです。その名人にとっては、餌よりも弾丸のほうがいい強化子な気はしますけども。
本題に戻って、
\[ r = \frac{b}{n} \]
と
\[ b = \frac{c.r}{\delta r + \frac{1}{a}} \]
を組み合わせると、反応率bは以下の式になります。
\[ b = \frac{c.}{\delta} - \frac{n}{\delta a} \]
FRスケジュールについてnを増やしていった時に、この式に従って反応率がどのように振る舞うかを見てみましょう。ただし、ここでいう反応率は、セッション時間に対しての総反応数というような意味だと思います(元論文のさらに元の論文に当たらねば確信はできないのですが)。
FR_rate_fun <- function(
delta = 0.32
,a = 200
,beta = 0.56
,n = 50
){
c <- c_FR_fun(beta = beta, n = n)
b <- (c / delta) - (n / (delta * a))
b <- ifelse(b<0, 0, b)
return(b)
}
##FR0というスケジュールは存在しないけど、グラフにする時のために0も含める
DF_FR_rate <- data.frame(
b = FR_rate_fun(n = 0:250, a = 200)
,n = 0:250
)
DF_FR_rate %>% ggplot(
aes(x = n, y = b)
) + geom_line()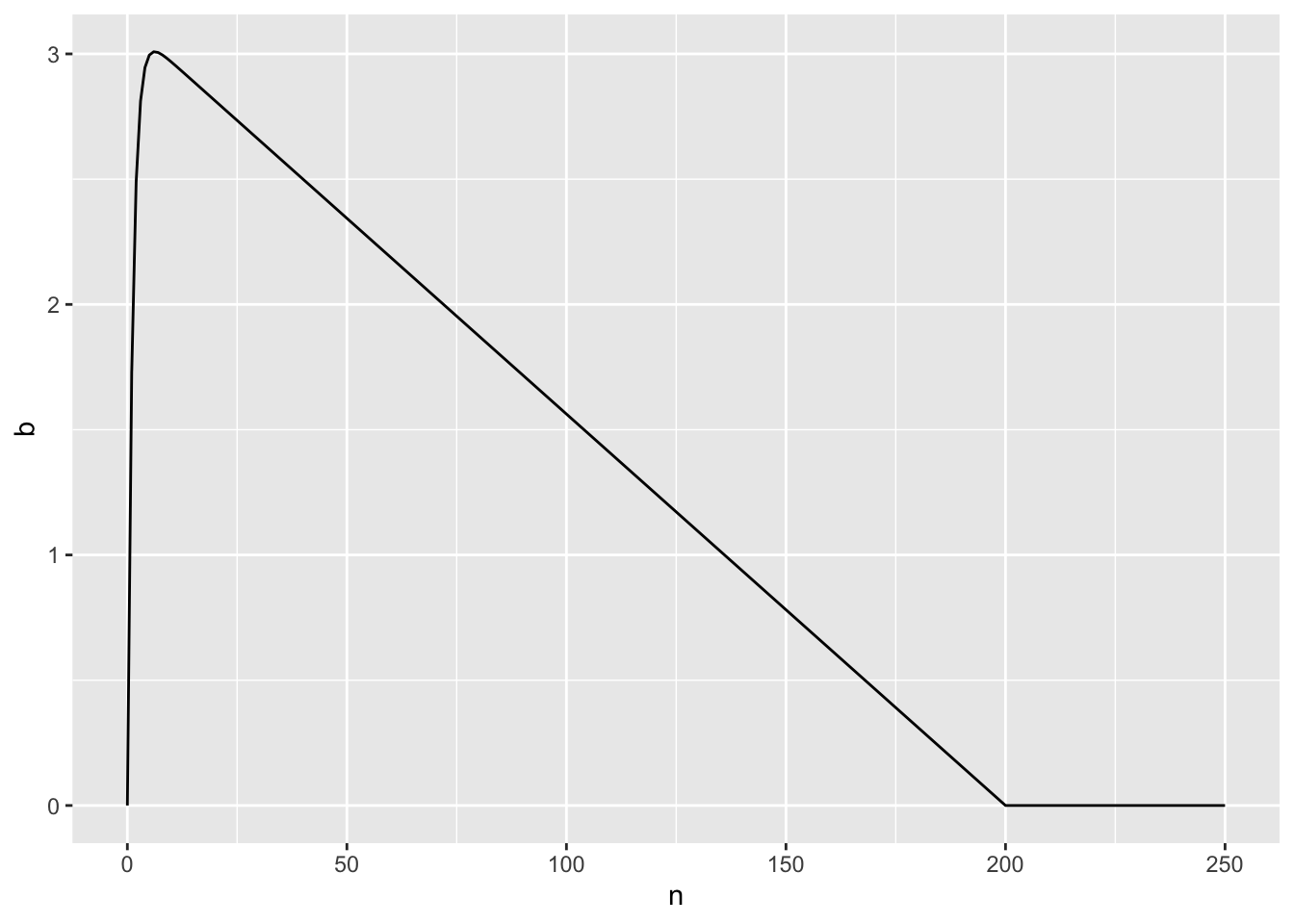
FRスケジュールでは、強化子提示までに必要な比率が少ないうちには、CRFの時よりも連続的な反応が生じ、比率が一定を超えるとPRPが生じて、そのPRPはnの値が大きいほど長くなるということが知られています。また、ある一定のnを超えると反応すらしなくなるということも知られています。
グラフを見てみましょう。n = 7くらいで反応率bは3回/秒という最大の値になります。仮にPRPが出現したとしても連打モードに入った時の反応率は3回/秒と同じだと仮定をします。すると、このグラフのn>7でのほぼ線形の反応率の減少は、PRPの長さによるものと解釈できるかもしれません。まあ、今回引用している Killeen and Sitomer (2003) の中ではPauseの話をしてはいないんですけどね。
続けてグラフを見ると、FR200を超えると、反応率が0になってしまいます。つまり反応しなくなったということですね。このFRスケジュールで反応しなくなる比率というのが特異的活性化aと一致するのではないかという指摘を Killeen and Sitomer (2003) はしています。
この特異的活性化aというのは、個体ごとに、あるいは、強化子ごとに、またその相互作用ごとに異なるようです。行動分析学者がブチギレそうな表現ですがわかりやすく書くならば、個々人で餌ごとに好き嫌いがあり、その好き嫌いによって活性化係数が変わるのではないだろうかという考えですね。
この活性化係数が変わることによって、二つの影響を及ぼします。一つは特異的活性化という名前の通り、その強化子がより好ましいのであれば(aがより大きいのであれば)、第一の原理で示したように、我々はより活発・覚醒的になるのかもしれません。確かに、より好きなものが与えられたらより活発になりそうですね。もう一つの影響というのが、FRn(もしくはPRn)スケジュールにおいて、その提示される強化子がより好ましいものであれば。より大きな比率nでも我慢して他の競合する行動に心を奪われずにレバーを押すことができるということなのかもしれません。たとえば、ヘロインなんかがもらえるなら、FR1000 でも永遠にレバーを押すシドヴィシャスは居そうですね(晩年はメサドンで我慢しようと彼も頑張ってはいたんですけどね)。シドヴィシャスにとってのヘロインの特異的活性化aは1000というわけです。
ここまでで重要なことというのはFRスケジュールにおいて、nが大きくなると結合係数のCFRn は1に近づくため、ある一定の最大反応率を超えたら、nが増えると直線的に反応率が減ってしまうということです。また、この反応率が0に、つまり反応しないようなnの数になる条件というのは、その強化子の持つ特異的活性化aと同値以上になるような時ということです。
VRスケジュールとはFRスケジュールを組み合わせたもの
すごいどうでもいい余談というか言い訳なんですが、僕修士まで社会心理学に属していたため、variableなスケジュールでどんなふうに比率を設定していたのかという学習心理学・行動分析学的な常識を知らなかったんですよね。当然スケジュール学習に特有の動物や人間の挙動をグラフで見たことはありますけどね。博士に入ってから、VRスケジュールにおいて、必要反応数を指数分布 幾何分布(2025-09-08修正。深夜テンションで作文してたのか、離散なの忘れてました。指数分布なのはVIですね)から取ってきているということを知りました。以下のグラフのイメージです。
#1000回レバー押して1セッション終わりという環境を想像。ちょっと酷な気はするけど。
VR_array <- rgeom(1000, 1/20) %>% round(.) ##この計算だと0回押して強化子が出る謎環境も生じるけど、修正面倒なので一旦このままで。
##平均何回押すと強化子出るか
VR_array %>% mean(.)## [1] 18.801##何回押すと強化子出るかの中央値
VR_array %>% median(.)## [1] 13##ヒストグラム
VR_array %>% hist()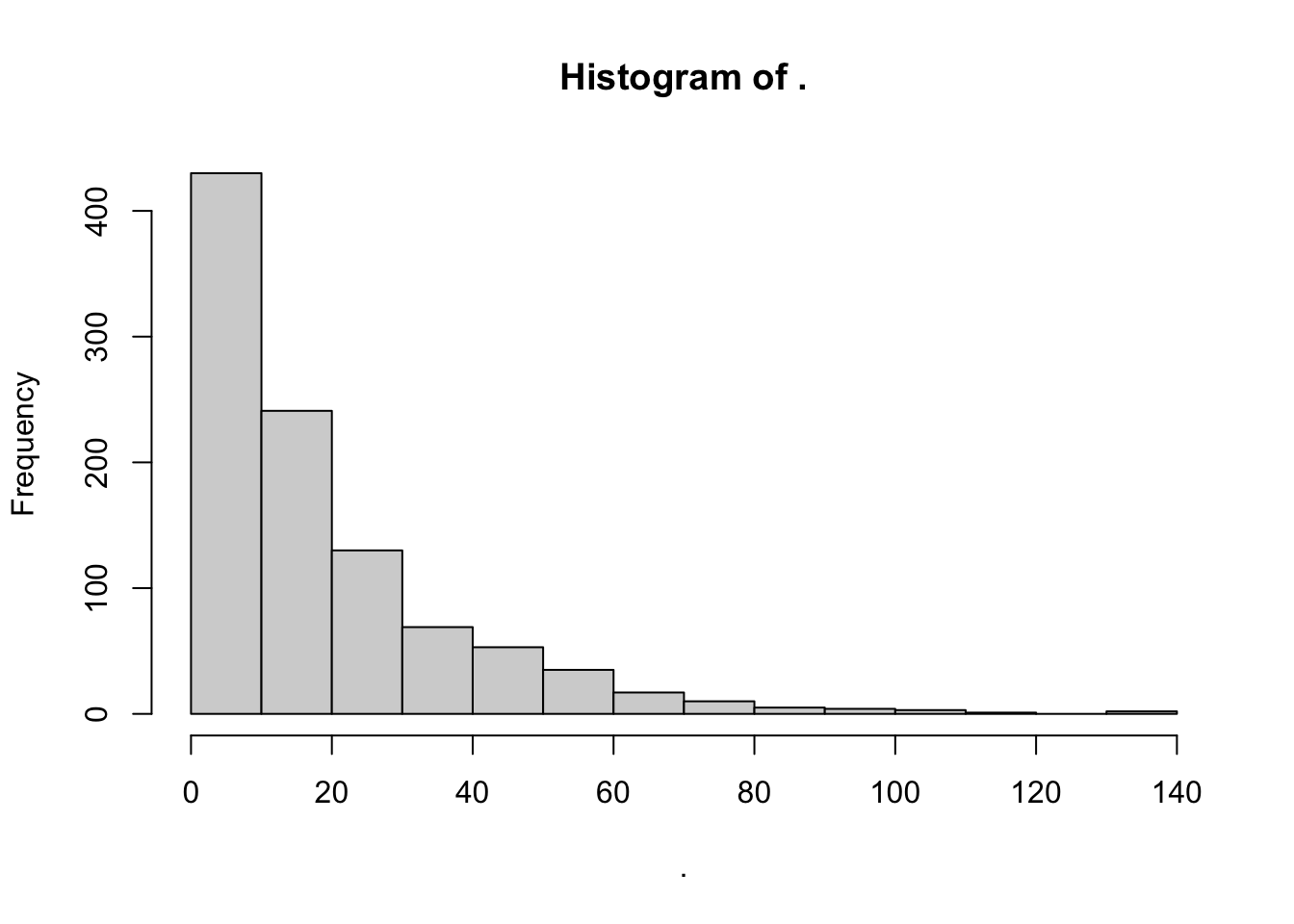
これの理由が、毎回のレバー押しでの当選確率を等しくするためなんですね。たとえば、VR20なら、毎回5%で強化子を獲得できるレバー押しをさせてあげると平均的には20回に1回強化子が得られるよ、という考えになっているということです。連チャンするかもしれないし、ずっと外れてるかもしれないけど、各試行での当選確率は等しく「見える」ということで、こんな指数乱数幾何分布を使っているんです。
ちなみに余談ですが、毎回のレバー押しで本当に確率抽選をしている場合(駅前のスキナー箱のレバーは一応この毎回独立の抽選になっているそうです、打たんから知らんけど。)には、Random Ratio:RRスケジュールと呼ばれるそうです。配列の要素を十分にシャッフルされているVR20でもRR20でも、スキナー箱に放り込まれた個体から見ると違いはわからないでしょうけどね。
random_ratio_fun <- function(
p = 1/20
,session = 1000
){
ratio <- NA %>% list()
for (i in 1:session) {
# 試行回数をカウント
count <- 0
# 当選するまでループを続ける
while (TRUE) {
count <- count + 1
# 乱数を生成し、当選確率と比較
if (runif(1) < p) {
break # 当選したらループを抜ける
}
}
# 当選までに要した試行回数を記録
ratio[[i]]<- count
}
ratio <- unlist(ratio)
return(ratio)
}
RR_array <- random_ratio_fun()
##平均何回押すと強化子出るか
RR_array %>% mean(.)## [1] 20.726##何回押すと強化子出るかの中央値
RR_array %>% median(.)## [1] 14##ヒストグラム
RR_array %>% hist()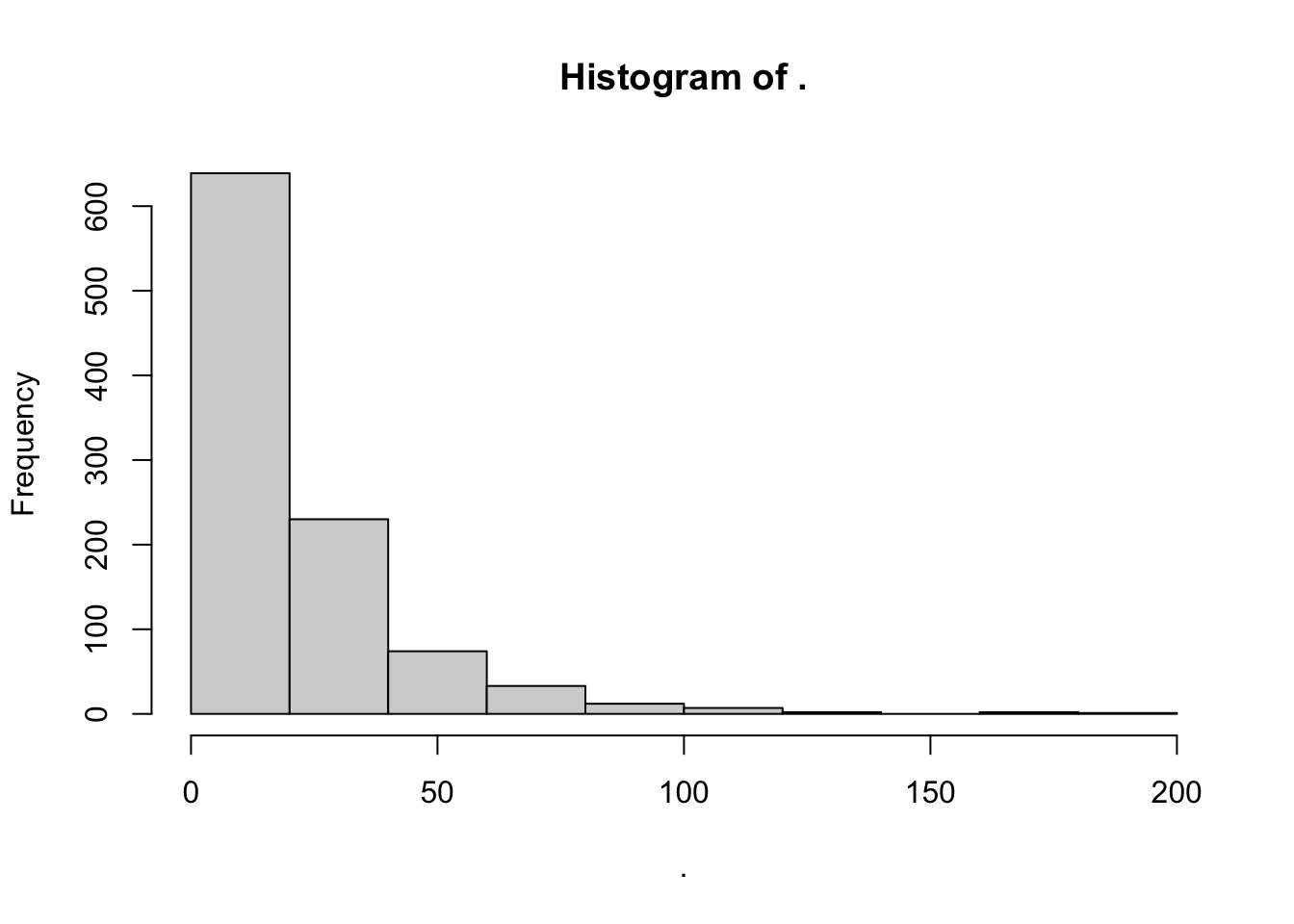
さて、こんなVRnスケジュールにおける結合係数CVRn をどのように出すかについて考えてみます。まずはVRスケジュールというものの本質的な部分を考えます。VRnスケジュールというのは、FR1, FR2, FR3, FR4,…FRn…,FR∞,というスケジュールが組み合わさって構成されていると考えられます。ここで∞というふうな添字が存在するのは、VRnスケジュールでは、毎回1/nの確率で抽選をしているだけで、その繰り返しの先には、理論上は∞回レバーを押しても強化子が出てこない可能性があるからです。実際のスキナー箱での実験では、有限回数に収めた環境を設定するでしょうから、あくまで無限というのは理論上の話ですけどね。
つまり、VRスケジュールでは、1回レバーを押して強化子を提示されるという経験や2回レバーを押して強化子が提示されるという経験というのが集約されて、CVRn が出来上がるという考え方になるわけですね。この集約の仕方については注意が必要です。VRスケジュールは指数乱数幾何分布の設定になっているわけですが、その真意は各試行での当選確率を一定にしたいからです。だから、その各試行での当選確率分の重みづけをした期待値に集約することになります。計算し終えると以下の式になります。ちょっとこの式の導出過程が論文内で書かれていなかったのでわからないですが、最初の式を立式できたらΣの足し算を展開していくと出せると思います。立式できたら追記します。
\[ C_{VR_n} = \frac{n}{n + \frac{1-\beta}{\beta}} \]
何はともあれこの式が出来上がったとして、このCVRn は、FRのそれと比較してどんな性質になっているかをグラフにしてみましょう。
c_VR_fun <- function(n = 100, beta =0.56){
c <- n /(n + ((1+beta)/beta))
return(c)
}
DF_VR_C <- data.frame(
c = c_VR_fun(n = 1:25)
,n = 1:25
,schedule = "VR"
)
##FRとの比較もしておく
DF_FR_VR_C <- DF_FR_C %>% mutate(
.
,schedule = "FR"
) %>% rbind(., DF_VR_C)
DF_FR_VR_C %>% ggplot(
aes(x = n, y = c, colour = schedule)
) + geom_line() 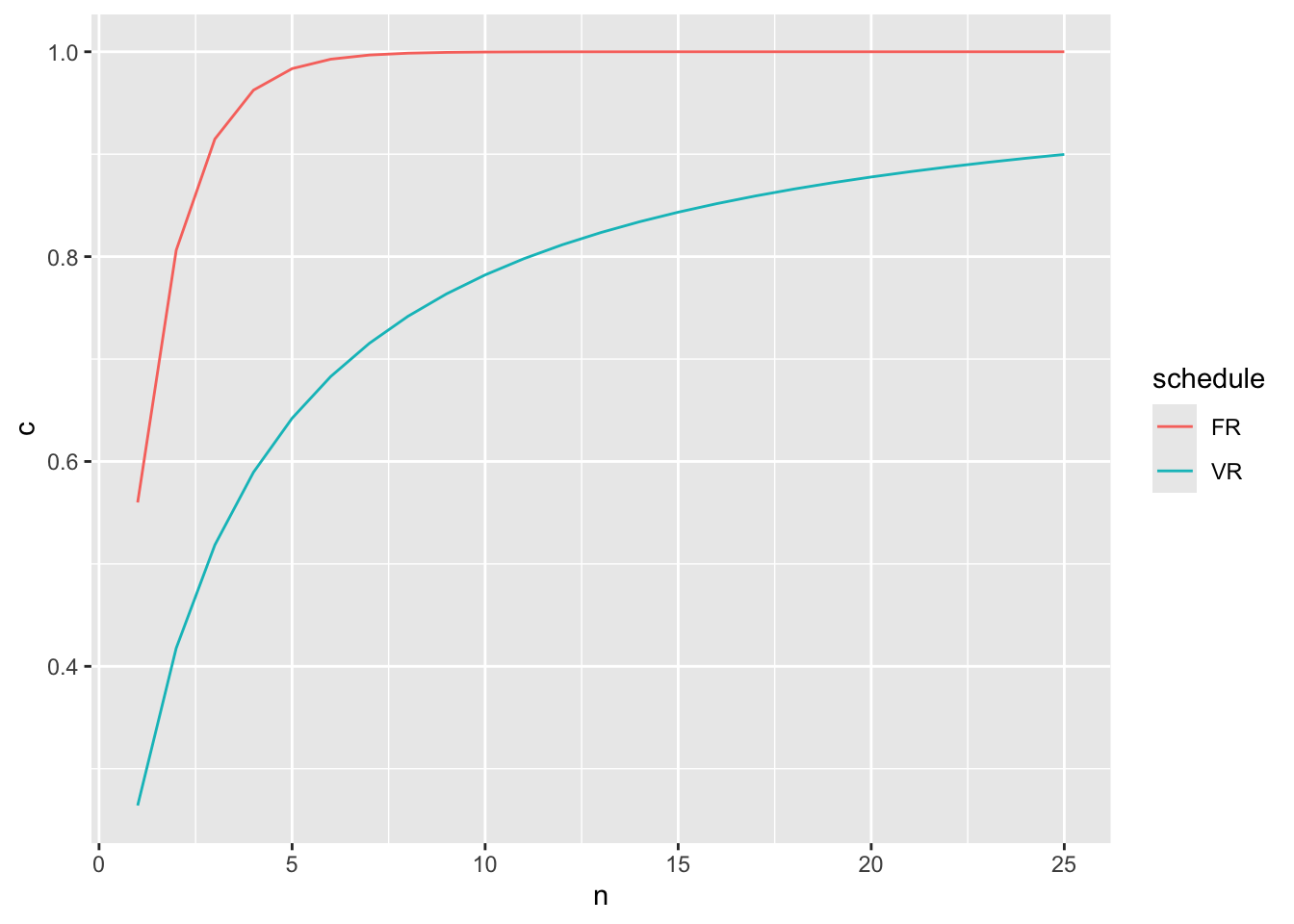
結合係数は、FRのものと比べて、立ち上がりが遅くなるし、いくらnが増えてもちょーっとずつ結合係数は増えていくんですね。当然と言えば当然ですね。
最後に、このCVRn という結合係数を利用して、VRスケジュールでの反応速度を出してみましょう。ここでも同じ比率のFRとの比較を行います。δやa、βといった他のパラメータは同じにしておきます。
VR_rate_fun <- function(
delta = 0.32
,a = 200
,beta = 0.56
,n = 50
){
c <- c_VR_fun(beta = beta, n = n)
b <- (c / delta) - (n / (delta * a))
b <- ifelse(b<0, 0, b)
return(b)
}
DF_VR_rate <- data.frame(
b = VR_rate_fun(n = 0:250)
,n = 0:250
,schedule = "VR"
)
DF_FR_VR_rate <- DF_FR_rate %>% mutate(
.
,schedule = "FR"
) %>% rbind(., DF_VR_rate)
##全部表示ver
DF_FR_VR_rate %>% ggplot(
aes(x = n, y = b, color = schedule)
) + geom_line()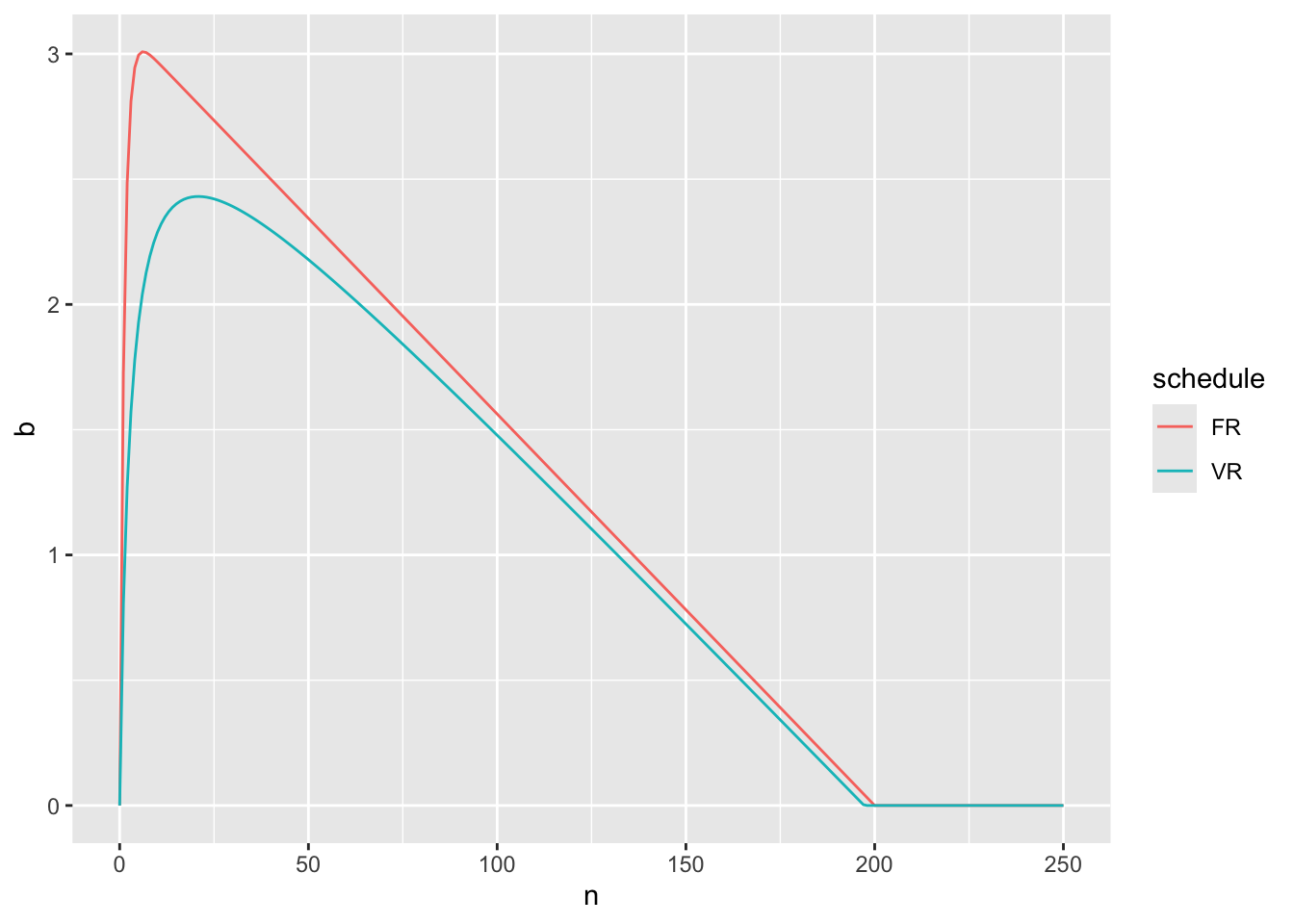
##一部表示ver
DF_FR_VR_rate %>% filter(
.
, n < 100
) %>% ggplot(
aes(x = n, y = b, color = schedule)
) + geom_line()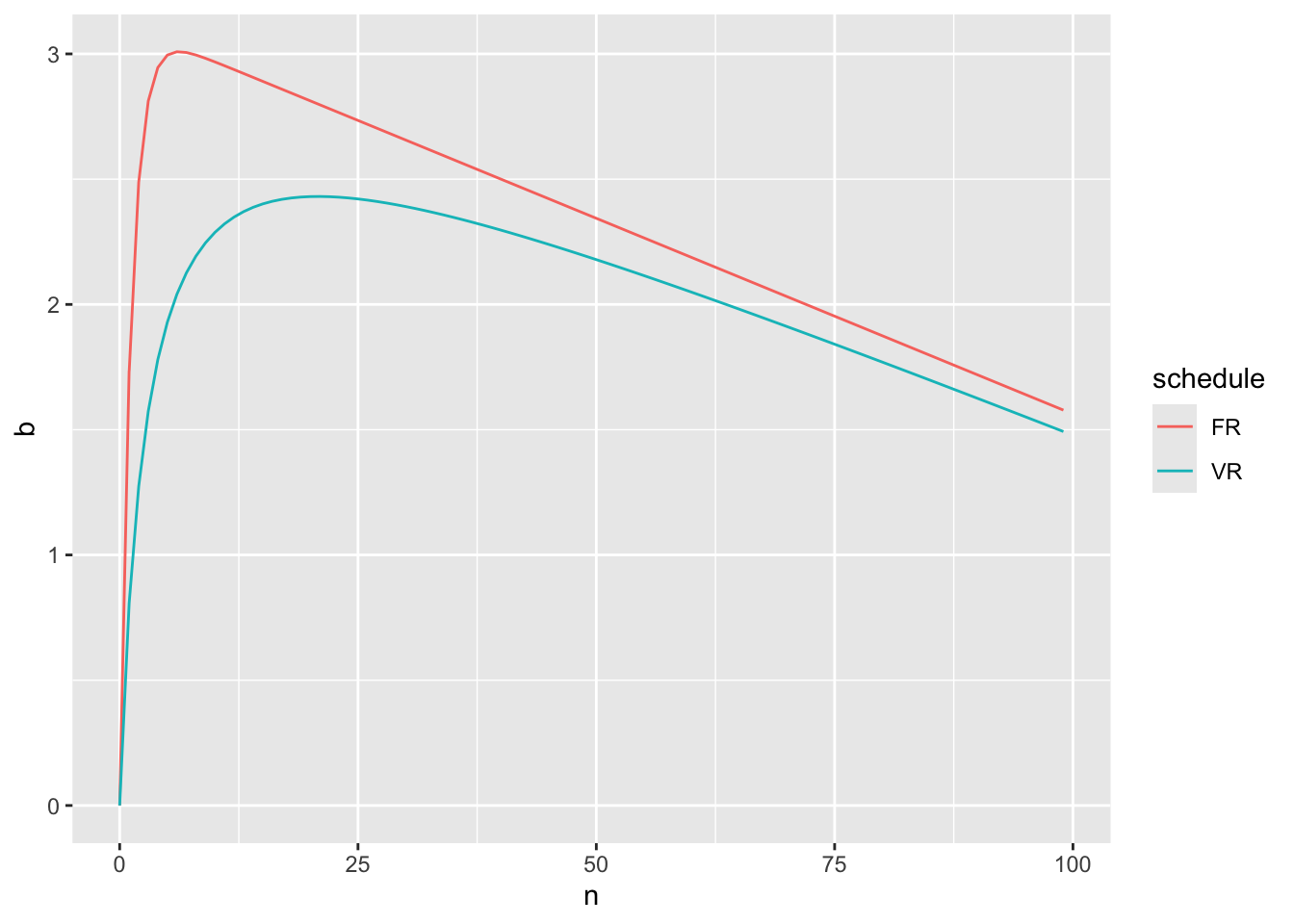
さて、2個目のグラフを見てみましょう。FRでは、最大の反応率になってから、直線的に反応率は低下していました。一方、VRではどうなるかというと、最大の反応率に至るまでにもVRよりもnの増大で遅れが生じます。また、最大反応率に至ってからもその減少の程度は直線的に減っていないことがわかります。これは、VRではFRよりも反応率が安定している性質の反映と理解することができます。
ただし、VRでもnが十分に大きくなるとやはりCVRn は1に近づくため、1枚目のグラフのように、100を超えたあたりからは直線的な反応率の減少が生じるようになってしまうのですね。
また、他のパラメータを変えてもいないので、x軸と触れるnの値というのもFRのaの値と同じになってしまいます。このモデルの真偽は置いておいて、直感的には、ボタンを押さなくなるFRnのnの比率よりも、ボタンを押さなくなるVRnのnの比率は高そうな気がするので、その仕様を追加してあげてモデルの改良ができそうな気はします。
まとめ
強化子によって生じる反応率というのは、各スケジュールに固有のCoupling 結合の係数によって調整されると考えます。このCoupling 結合という考え方を元にして、強化学習モデルを拡張させることも可能な気がしました。余力ある時に作ってみようかな。
今回引用した Killeen and Sitomer (2003) では比率 ratioスケジュールについての説明しか行われていませんでした。また、休止、特にPRPや各レバー押しの試行の間のIRTの分布がどのような数理的な原則で生み出されているのかについては触れられていませんでした。休止やIntervalスケジュールは、2023年に引退前の総集編みたいな論文(Killeen 2023)を出しているので、そちらを読んで理解をしたいです。手に入れてチラッと読みましたが、PRPの数式が本当に何を書いているのかわからなかったので、気合い入れて読みたいなと思っています。
以下は完全な余談です。僕はスロットは好きではありません。ギャンブルは競馬が好きです、お馬さん可愛いので。ただ、スケジュール研究、ましてやスキナー箱のそれをするからには、スロット打たなきゃなと最近強く思っています。昔に打ったことはありますが、レバー叩いたら精霊に「頑張って」って言われて変なコンビがいつも降ってきて頑張る気力を奪われて飽きました。ちなみに、その Killeen (2023) の論文では、弁別刺激を提示して強化子が来るかどうかの予告をした事態でのPRPの長さを調べた研究を引用してたりします。パチスロ以外は打ったことないので映像しか見たことないですが、カジノスロットでも激アツ予告ってあるらしいですからね、こういう発想を獲得するためにもやっぱりスロット打つしかないのかな。
みなさんも、VR(RR)スケジュールにはお気をつけて、ほどほどに確率的な強化子獲得のための意思決定を楽しみましょう。今後も僕はオッズ10倍くらいの単勝一本勝負競馬だけでいいかな。